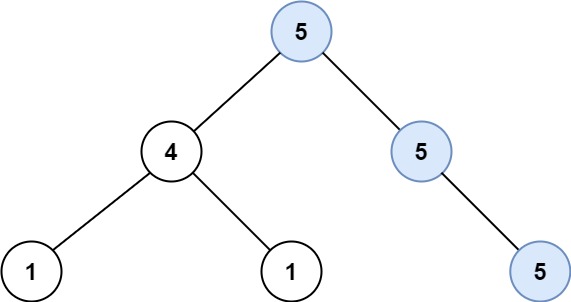
1
2

输入：root = [5,4,5,1,1,5]
输出：2

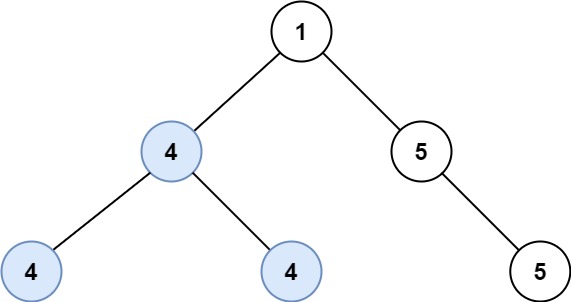
1
2

输入：root = [1,4,5,4,4,5]
输出：2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

class Solution {
public:
    /**
     * @brief 解题思路
     * @param 递归法
     * 1. 经过一个节点的同值路径分为左右两个部分：左路径长度 + 右路径长度；
     * 2. 左路径长度 = 0            左子节点与当前节点不同值
     *             = 左子节点路径长度 + 1 (左子节点与当前节点同值)
     *    右路径长度 = 0            右子节点与当前节点不同值
     *             = 左子节点路径长度 + 1 (右子节点与当前节点同值)
     *  3. 最长同值路径 = max(左路径长度+右路径长度)
     */
    int longestUnivaluePath(TreeNode* root) {
        int longestPath = 0;

        getUnivalPathWithParent(root, -2000, longestPath);

        return longestPath;
    }

    /**
     * @brief 深度遍历二叉树, 计算以node节点为一个端点的最长同值路径的路径长度
     * @param[in] node: 
     * @param[in] parentVal:
     * @param[context] longestPath: 
     * @param[out] 
     */
    int getUnivalPathWithParent(TreeNode* node, int parentVal, int& longestPath) {
        if (!node) {
            return 0;
        }

        // 以当前节点为端点的左子树的同值路径长度
        int leftPath = getUnivalPathWithParent(node->left, node->val, longestPath);
        // 以当前节点为端点的右子树的同值路径长度
        int rightPath = getUnivalPathWithParent(node->right, node->val, longestPath);

        int curNodeUnivalPath = leftPath + rightPath;
        // 经过当前节点的最长路径长度
        if (curNodeUnivalPath > longestPath) {
            longestPath = curNodeUnivalPath; 
        }
        // 如果当前节点和父节点同值，则到父节点的同值长度为：
        // 左右子树最长同值路径中更长的一个 +1
        if (node->val == parentVal) {
            return leftPath>rightPath?leftPath+1:rightPath+1;
        } else { //当前节点和父节点不同值
            return 0;
        }

        return 0;
    }
};