最小高度树

Category	Difficulty	Likes	Dislikes
algorithms	Medium (42.58%)	790	-

Tags

breadth-first-search | graph

Companies

google

树是一个无向图，其中任何两个顶点只通过一条路径连接。换句话说，一个任何没有简单环路的连通图都是一棵树。

给你一棵包含 n 个节点的树，标记为 0 到 n - 1 。给定数字 n 和一个有 n - 1 条无向边的 edges 列表（每一个边都是一对标签），其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边。

可选择树中任何一个节点作为根。当选择节点 x 作为根节点时，设结果树的高度为 h 。在所有可能的树中，具有最小高度的树（即，min(h)）被称为 最小高度树 。

请你找到所有的 最小高度树 并按 任意顺序 返回它们的根节点标签列表。

树的高度是指根节点和叶子节点之间最长向下路径上边的数量。

示例 1：

1
2
3
输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 2：

1
2
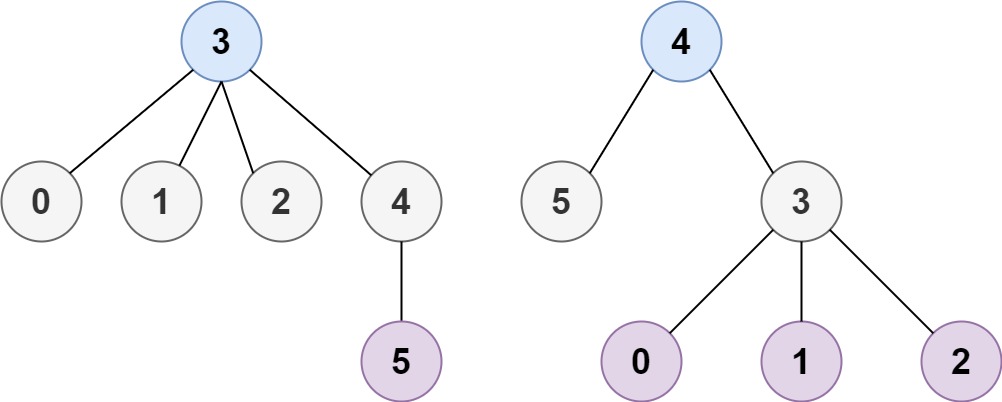
输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

提示：

1 <= n <= 2 * 104
edges.length == n - 1
0 <= ai, bi < n
ai != bi
所有 (ai, bi) 互不相同
给定的输入保证是一棵树，并且 不会有重复的边

Discussion | Solution

解法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
struct Solution;
// @lc code=start
impl Solution {
    /// ## 解题思路
    /// - 广度优先搜索
    /// 1. 遍历edges, 计算每个节点的入度;
    /// 2. 收集所有入度为1的为叶节点为一个起始集合;
    /// 3. 从叶节点集合开始, 依次剥离各层邻接节点;
    /// 4. 最后剩余的一层节点即为最小高度根节点集;
    pub fn find_min_height_trees(n: i32, edges: Vec<Vec<i32>>) -> Vec<i32> {
        use std::collections::VecDeque;

        if n == 1 {
            return vec![0];
        }

        // 1. 遍历edges, 计算各个节点的入度
        let mut in_count = vec![0; n as usize];
        let mut nodes = vec![vec![]; n as usize];
        for edge in &edges {
            let (from, to) = (edge[0] as usize, edge[1] as usize);
            in_count[from] += 1;
            in_count[to] += 1;
            nodes[from].push(to);
            nodes[to].push(from);
        }

        // 收集入度为1的所有叶子节点
        let mut leaves = in_count
            .iter()
            .enumerate()
            .filter(|(_, &d)| d == 1)
            .map(|(id, _)| id as i32)
            .collect::<VecDeque<_>>();

        let mut remain = n as usize;

        // 从外向内逐级剥离各层叶子节点
        // 剩余节点数 <= 2时退出
        while remain > 2 {
            remain -= leaves.len();
            // 取出当前层的所有叶节点
            for _ in 0..leaves.len() {
                let from = leaves.pop_front().unwrap() as usize;
                // 当前叶节点的所有上级节点
                for &to in &nodes[from] {
                    in_count[to] -= 1; //上级节点入度-1

                    // 如果入度为1,
                    if in_count[to] == 1 {
                        // 则该节点为下一级的叶子节点
                        leaves.push_back(to as i32);
                    }
                }
            }
        }

        leaves.into_iter().collect::<Vec<i32>>()
    }
}
// @lc code=end

最小高度树

最小高度树

解法

相关文章：