Justice's Site

搜索二维矩阵 II

 滴水穿石  158  1 分钟

搜索二维矩阵 II

CategoryDifficultyLikesDislikes
algorithmsMedium (52.80%)1301-
Tags

binary-search | divide-and-conquer

Companies

amazon | apple | google

编写一个高效的算法来搜索 <em>m</em> x <em>n</em> 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

  • 每行的元素从左到右升序排列。
  • 每列的元素从上到下升序排列。

示例 1：

1
2

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

1
2

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

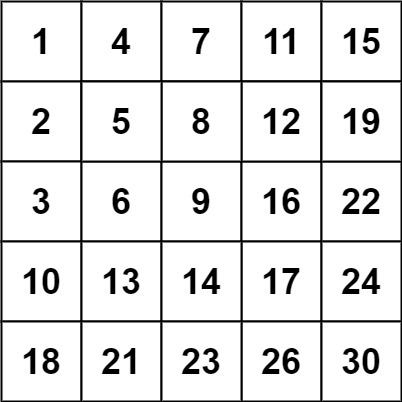
提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= n, m <= 300
  • -10<sup>9</sup> <= matrix[i][j] <= 10<sup>9</sup>
  • 每行的所有元素从左到右升序排列
  • 每列的所有元素从上到下升序排列
  • -10<sup>9</sup> <= target <= 10<sup>9</sup>

Discussion | Solution

解法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

// @lc code=start
impl Solution {
    /// ## 解题思路
    /// - 二分查找(z字形搜索)
    /// 1. 设置查找起点为(x,y) = (0, n-1)矩阵右上角;
    /// 2. 如果 target == matrix[x][y], 则找到target, 返回true;
    /// 3. 如果 target > matrix[x][y], 则target在当前元素下方, y+=1;
    /// 4. 否则 target < matrix[x][y], target在当前元素左侧, x-=1;
    pub fn search_matrix(matrix: Vec<Vec<i32>>, target: i32) -> bool {
        let (m, n) = (matrix.len(), matrix[0].len());
        let (mut r, mut c) = (0, n - 1);
        while (0..m).contains(&r) && (0..n).contains(&c) {
            match target.cmp(&matrix[r][c]) {
                std::cmp::Ordering::Equal => return true,
                std::cmp::Ordering::Greater => r += 1,
                _ => c -= 1,
            }
        }

        return false;
    }
}
// @lc code=end

struct Solution;

相关文章：