天际线问题

问题描述

Category	Difficulty	Likes	Dislikes
algorithms	Hard (39.25%)	93	-

Tags

divide-and-conquer | heap | binary-indexed-tree | segment-tree | line-sweep

Companies

facebook | google | microsoft | twitter | yelp

城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度，请返回 *由这些建筑物形成的**天际线** 。

每个建筑物的几何信息由数组 buildings 表示，其中三元组 buildings[i] = [lefti, righti, heighti] 表示：

lefti 是第 i 座建筑物左边缘的 x 坐标。
righti 是第 i 座建筑物右边缘的 x 坐标。
heighti 是第 i 座建筑物的高度。

你可以假设所有的建筑都是完美的长方形，在高度为 0 的绝对平坦的表面上。

天际线 应该表示为由 “关键点” 组成的列表，格式 [[x1,y1],[x2,y2],...] ，并按 **x 坐标 **进行排序。 关键点是水平线段的左端点 。列表中最后一个点是最右侧建筑物的终点，y 坐标始终为 0 ，仅用于标记天际线的终点。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

注意： 输出天际线中不得有连续的相同高度的水平线。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[...[2 3], [4 5], [12 7], ...]

示例 1：

1
2
3
4
5
输入：buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出：[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释：
图 A显示输入的所有建筑物的位置和高度，
图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。

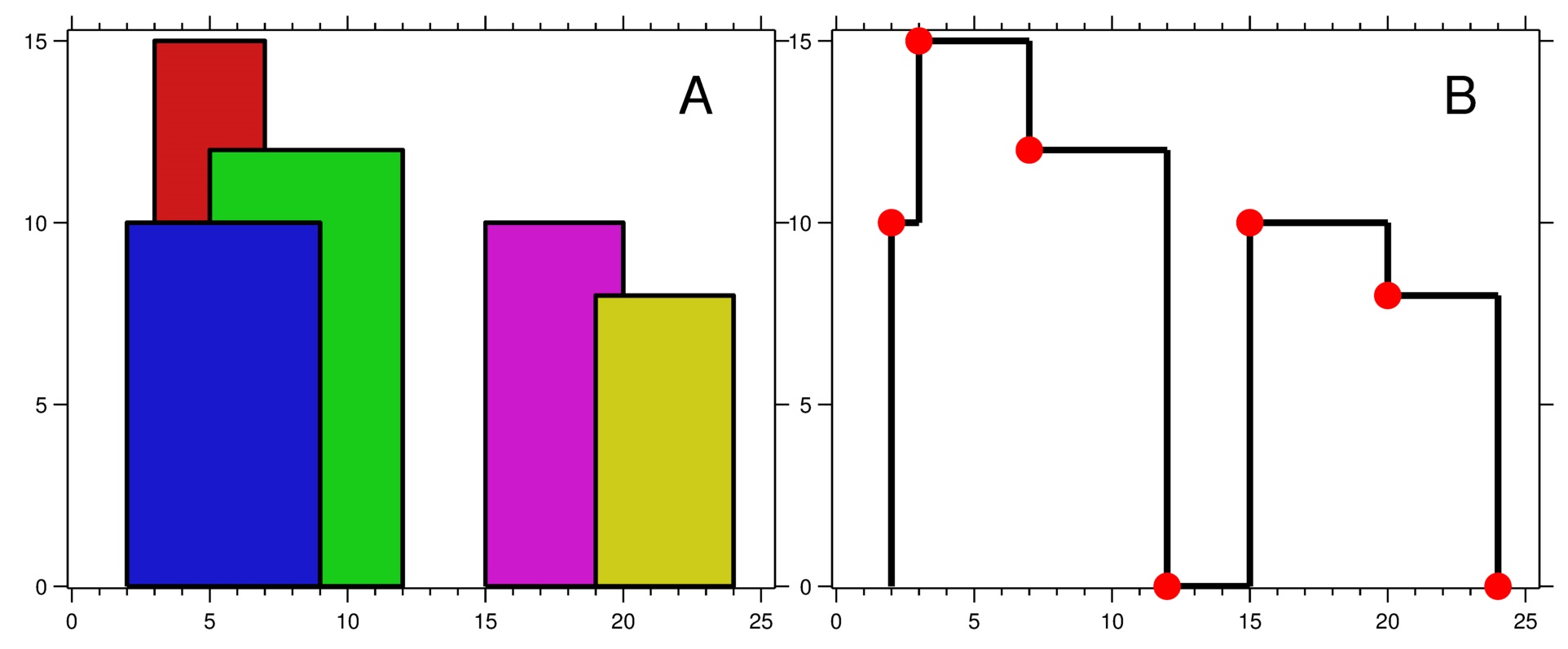
示例 2：

1
2
输入：buildings = [[0,2,3],[2,5,3]]
输出：[[0,3],[5,0]]

提示：

1 <= buildings.length <= 104
0 <= lefti < righti <= 231 - 1
1 <= heighti <= 231 - 1
buildings 按 lefti 非递减排序

说明:

任何输入列表中的建筑物数量保证在 [0, 10000] 范围内。
输入列表已经按左 x 坐标 Li 进行升序排列。
输出列表必须按 x 位排序。
输出天际线中不得有连续的相同高度的水平线。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[...[2 3], [4 5], [12 7], ...]

Discussion | Solution

解法

分治+归并

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
struct Solution;

// @lc code=start
impl Solution {
    /// ## 解题思路
    /// - 分治+归并
    /// 1. 整体所有矩形的天际线 = merge(左半部分矩形天际线, 右半部分天际线)
    /// 2. 如此递归, 直到左右为1个矩形, 此时天际线为:
    ///             [
    ///                [buildings[0][0], buildings[0][2]],
    ///                [buildongs[0][1], buildings[0][2]]
    ///             ];
    /// 3. merge流程:
    ///    待merge: left_skylines: [ [xl1, yl1], [xl2, yl2], [xl3, yl3]...]
    ///            right_skylines: [ [xr1, yr1], [xr2, yr2], ...]
    ///    3.1 分别设置指针(l, r), 指向左右子集的开始;
    ///    3.2 合并时, 选择左右集中x坐标较小的作为转折点的x坐标, 对应的h中高的为y坐标;
    ///    3.3 如果新转折点和上一个转折点的y坐标相同, 则新转折点和上一个转折点在同一个横线上, 需要忽略新转折点;
    ///    3.4 如果新转折点和上一个转折点的x坐标相同, 则新转折点和上一个转折点在同一个竖线上, 则只需更新上一个转折点点y坐标为新的y;
    ///    3.5 其他情况下, 直接将新转折点加入到总合并集的尾部;
    pub fn get_skyline(buildings: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        // 获取指定范围[start, end)内的天际线
        fn get_skyline_by_range(buildings: &[Vec<i32>], start: usize, end: usize) -> Vec<Vec<i32>> {
            if end - start < 1 {
                return vec![];
            } else if end - start == 1 {
                return vec![
                    vec![buildings[start][0], buildings[start][2]],
                    vec![buildings[start][1], 0],
                ];
            }

            // r - l > 1
            let mut res: Vec<Vec<i32>> = vec![];
            let mid = (start + end) >> 1;
            let left_res = get_skyline_by_range(buildings, start, mid);
            let right_res = get_skyline_by_range(buildings, mid, end);
            let (mut x, mut hl, mut hr) = (0, 0, 0);
            let (mut l, mut r) = (0, 0);
            // 合并 left_res, right_res
            while l < left_res.len() || r < right_res.len() {
                // 如果right区间合并完了或者左边区间x坐标 < 右边的x坐标
                if r == right_res.len() || (l < left_res.len() && left_res[l][0] < right_res[r][0])
                {
                    x = left_res[l][0];
                    hl = left_res[l][1];
                    l += 1;
                } else {
                    x = right_res[r][0];
                    hr = right_res[r][1];
                    r += 1;
                }
                // 转折点高度为左右两个待合并点中高的那个
                let h = std::cmp::max(hl, hr);
                let len = res.len();
                // 如果新转折点高度和上一个转折点的相同, 则跳过
                if len > 0 && h == res[len - 1][1] {
                    continue;
                }
                // 如果新转折点x坐标和上一个相同, 则更新上一个y坐标;
                if len > 0 && x == res[len - 1][0] {
                    res[len - 1][1] = h;
                } else {
                    // 否则,将(x, h)作为新的转折点, 加入到结果集中
                    res.push(vec![x, h]);
                }
            }

            res
        }

        get_skyline_by_range(&buildings, 0, buildings.len())
    }
}
// @lc code=end

扫描线法

使用扫描线，从左至右扫过。

如果遇到左端点，将高度入优先队列，如果遇到右端点，则将高度从优先队列中删除。

使用 last 变量记录上一个转折点。

可以参考下面的图，扫描线下方的方格就是堆。

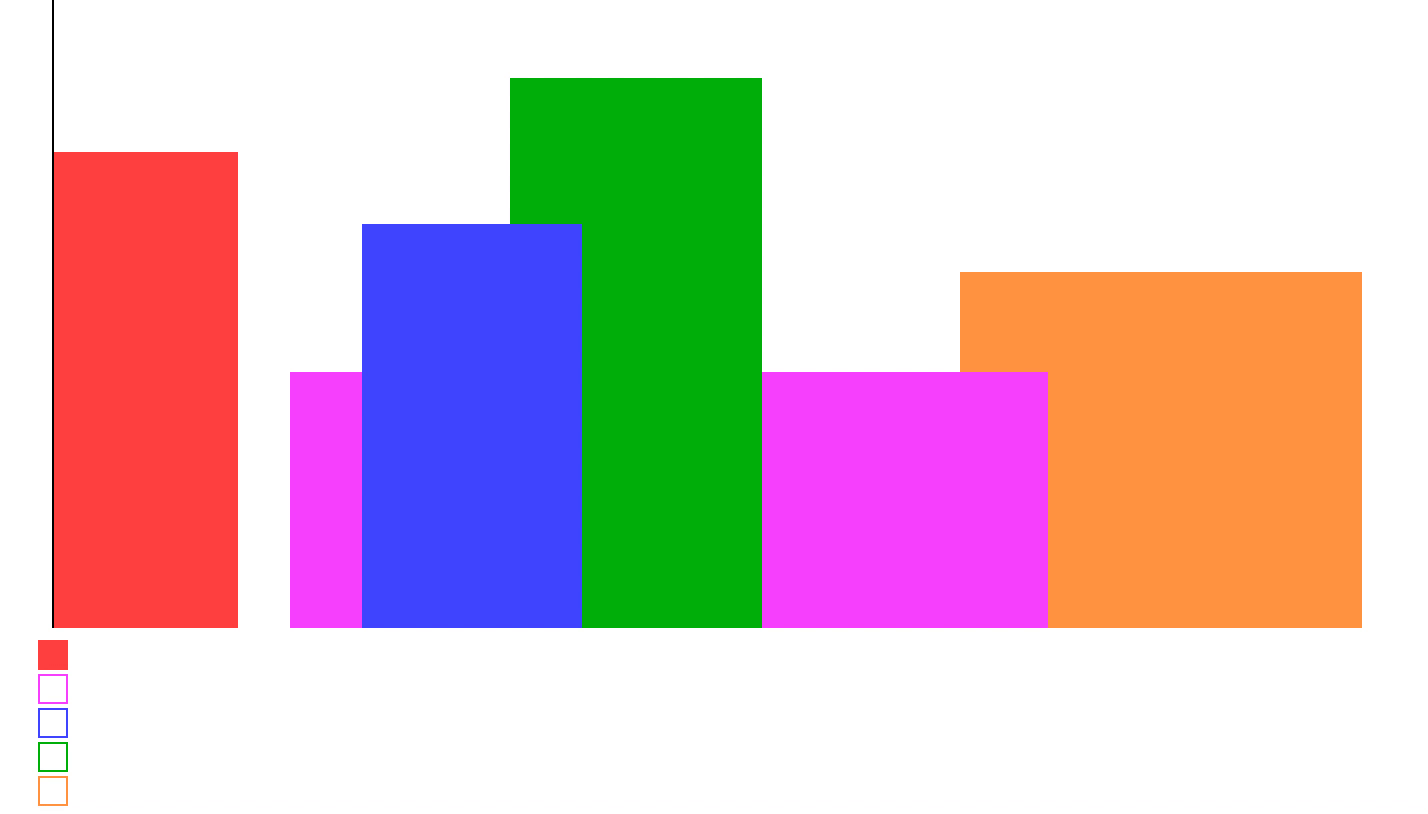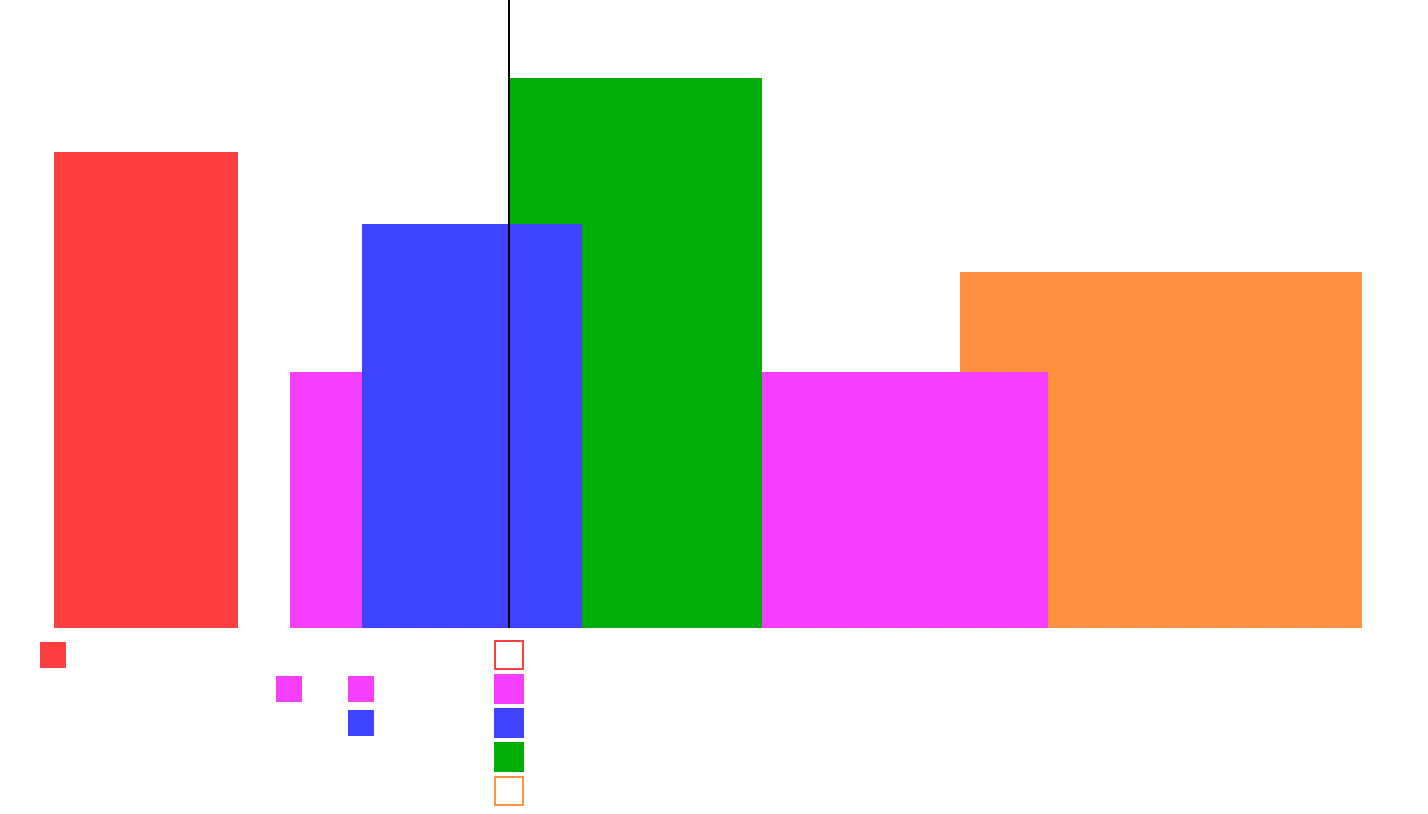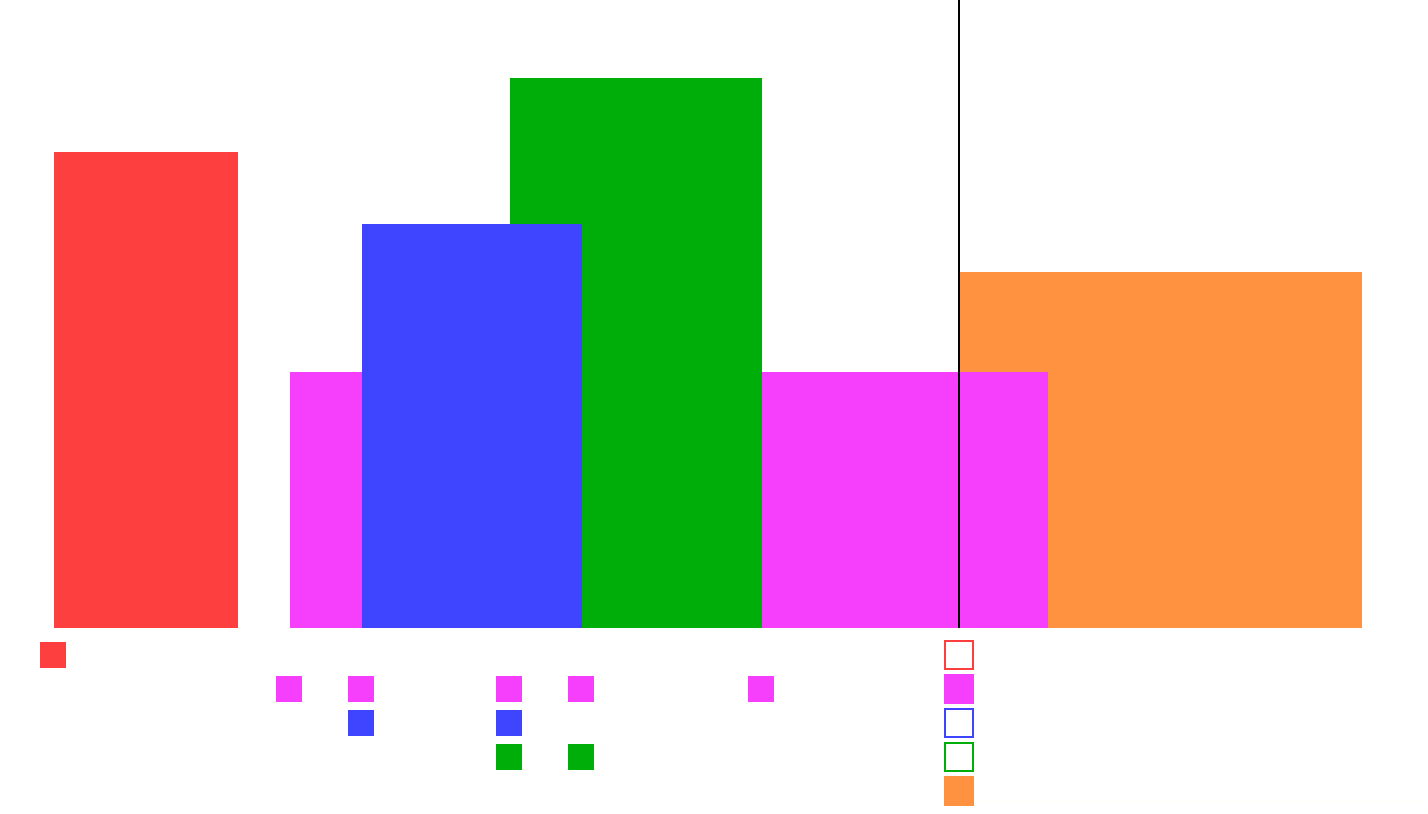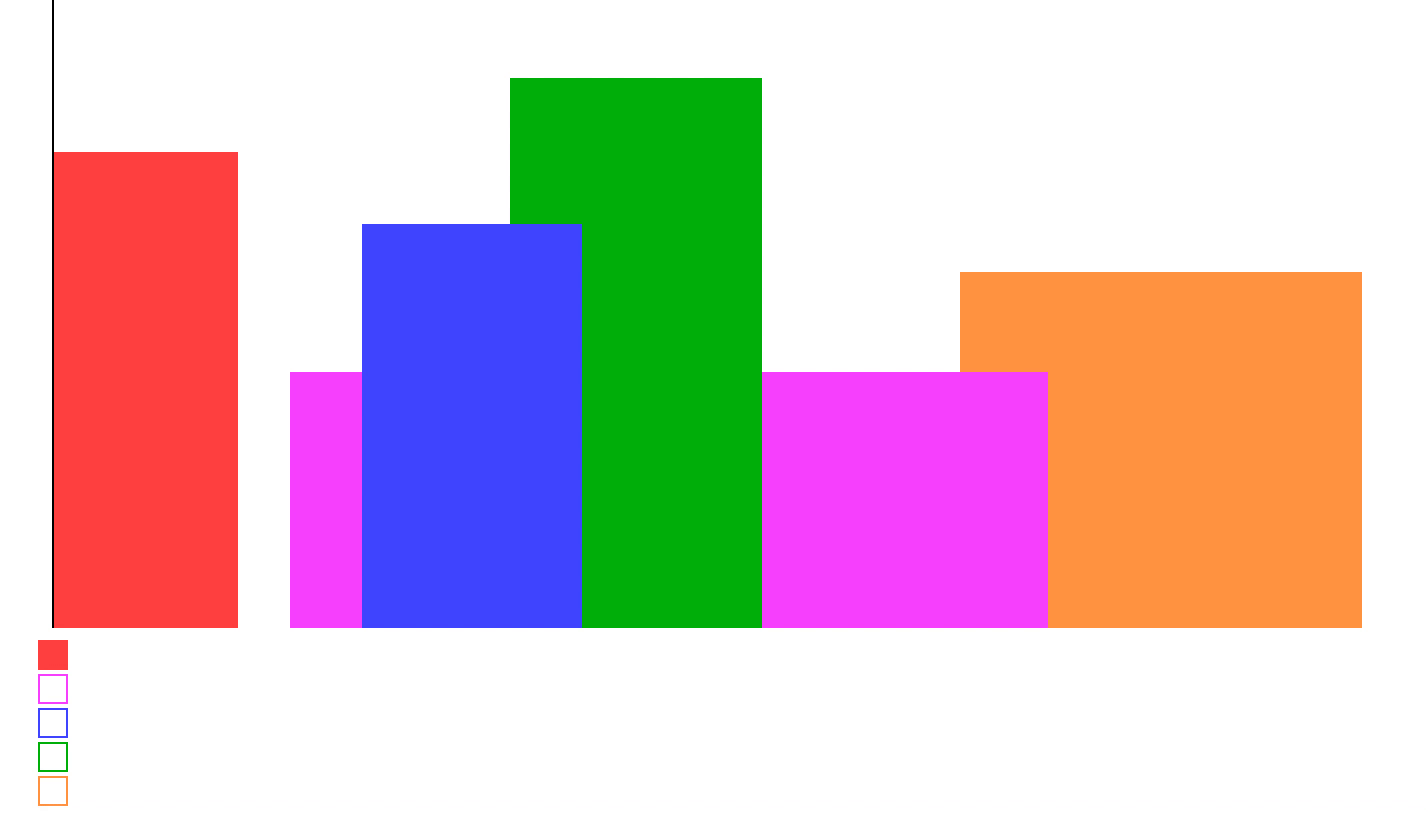
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def getSkyline(self, buildings) :
        res = []        # results
        last = [0, 0]   #
        heights = []    #
        l_heights = [ (build[0], -build[2]) for build in buildings]
        r_heights = [ (build[1], build[2]) for build in buildings]
        all_heights = sorted( l_heights + r_heights)
        for x, y in all_heights:
            if y < 0:   #scan left point
                heights.append(-y)
            else:
                i = heights.index(y)
                heights.pop(i)
            maxHeight = 0
            if len(heights) > 0:
                maxHeight = max(heights)
            if last[1] != maxHeight:
                last = [x, maxHeight]
                res.append(last)
        return res

天际线问题

天际线问题

问题描述

解法

分治+归并

扫描线法

相关文章：