子树中标签相同的节点数

Category	Difficulty	Likes	Dislikes
algorithms	Medium (31.49%)	57	-

Tags

Unknown

Companies

Unknown

给你一棵树（即，一个连通的无环无向图），这棵树由编号从 0 到 n - 1 的 n 个节点组成，且恰好有 n - 1 条 edges 。树的根节点为节点 0 ，树上的每一个节点都有一个标签，也就是字符串 labels 中的一个小写字符（编号为 i 的节点的标签就是 labels[i] ）

边数组 edges 以 edges[i] = [ai, bi] 的形式给出，该格式表示节点 ai 和 bi 之间存在一条边。

返回一个大小为 n 的数组，其中 ans[i] 表示第 i 个节点的子树中与节点 i 标签相同的节点数。

树 T 中的子树是由 T 中的某个节点及其所有后代节点组成的树。

示例 1：

1
2
3
4
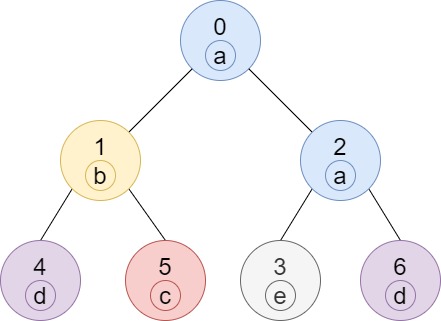
输入：n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
输出：[2,1,1,1,1,1,1]
解释：节点 0 的标签为 'a' ，以 'a' 为根节点的子树中，节点 2 的标签也是 'a' ，因此答案为 2 。注意树中的每个节点都是这棵子树的一部分。
节点 1 的标签为 'b' ，节点 1 的子树包含节点 1、4 和 5，但是节点 4、5 的标签与节点 1 不同，故而答案为 1（即，该节点本身）。

示例 2：

1
2
3
4
5
6
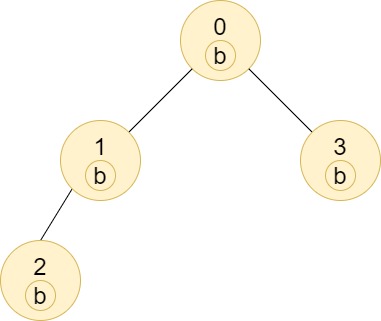
输入：n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
输出：[4,2,1,1]
解释：节点 2 的子树中只有节点 2 ，所以答案为 1 。
节点 3 的子树中只有节点 3 ，所以答案为 1 。
节点 1 的子树中包含节点 1 和 2 ，标签都是 'b' ，因此答案为 2 。
节点 0 的子树中包含节点 0、1、2 和 3，标签都是 'b'，因此答案为 4 。

示例 3：

1
2
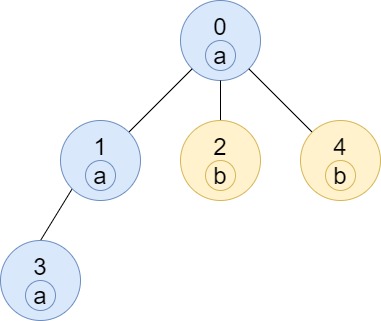
输入：n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
输出：[3,2,1,1,1]

提示：

1 <= n <= 10^5
edges.length == n - 1
edges[i].length == 2
0 <= ai, bi < n
ai != bi
labels.length == n
labels 仅由小写英文字母组成

Discussion | Solution

解法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#[derive(Clone)]
struct Node {
    edges: Vec<i32>,
    label: u8,
    visited: bool,
}

impl Solution {
    /// ## 解题思路
    /// * 深度优先搜索
    /// 1. 
    pub fn count_sub_trees(n: i32, edges: Vec<Vec<i32>>, labels: String) -> Vec<i32> {
        // 初始化每一个节点的邻居矩阵
        let mut graphic: Vec<Node> = Vec::with_capacity(n as usize);
        graphic.resize(n as usize, Node {
            edges: Vec::new(),
            label: 0,
            visited: false,
        });
        // 初始化各个节点的边
        for edge in edges {
            graphic[edge[0] as usize].edges.push(edge[1]);
            graphic[edge[1] as usize].edges.push(edge[0]);
        }
        // 初始化各个节点的label
        for (i, l) in labels.as_bytes().into_iter().enumerate() {
            graphic[i].label = l - b'a';
        }

        let mut result: Vec<i32> = Vec::with_capacity(n as usize);
        result.resize(n as usize, 0);

        //
        Solution::dfs(0, &mut graphic, &mut result);

        result
    }

    fn dfs(node: i32, graphic: &mut [Node], result: &mut [i32]) -> [i32; 26] {
        let current_node = &mut graphic[node as usize];
        current_node.visited = true;
        let label = current_node.label as usize;
        let mut count = [0_i32; 26];
        count[label] += 1;

        for i in 0..current_node.edges.len() {
            let child = graphic[node as usize].edges[i];
            if !graphic[child as usize].visited {
                let cc = Solution::dfs(child, graphic, result);
                for j in 0..26 {
                    count[j] += cc[j];
                }
            }
        }

        result[node as usize] = count[label];
        count
    }
}

子树中标签相同的节点数

子树中标签相同的节点数

解法

相关文章：