专题：树状数组

简介

树状数组是一种用来计算区间和(涉及元素修改)的高效数据结构，其查询(计算区间和)和更新(修改单个元素值)操作都能只有O(log(n))的时间复杂度。

问题分析

对于一个数组nums[], 有两种基本计算需求：

• a. 修改其中某一个元素nums[i]: update(i, new_val)；

• b. 获取某一区间和: range_sum(nums[a..b])；

通常满足以上2种需求有如下两种算法：

• a. 直接在原数组nums上计算;

• b. 通过前缀和数组prefix_sums来计算(prefix_sums[i]=sum(nums[0..i]))；

两种算法的时间复杂度对比如下：

可以发现，上述两种不同算法对于update和range_sum这两种操作只能兼顾一个的性能。

而树状数组可以很好的对这两种操作进行平衡，将时间复杂度均达到O(log(n))，是二者的一个折衷。

树状数组由来

首先，对于普通数组A[]，将其按二叉树进行组织如下：

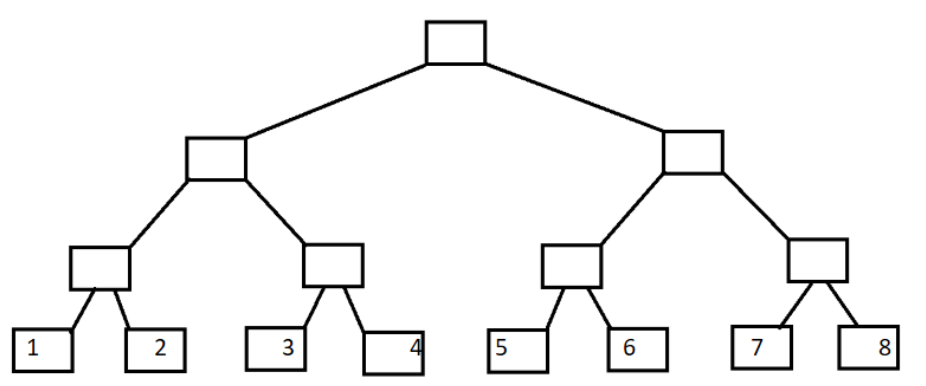
转换一下：

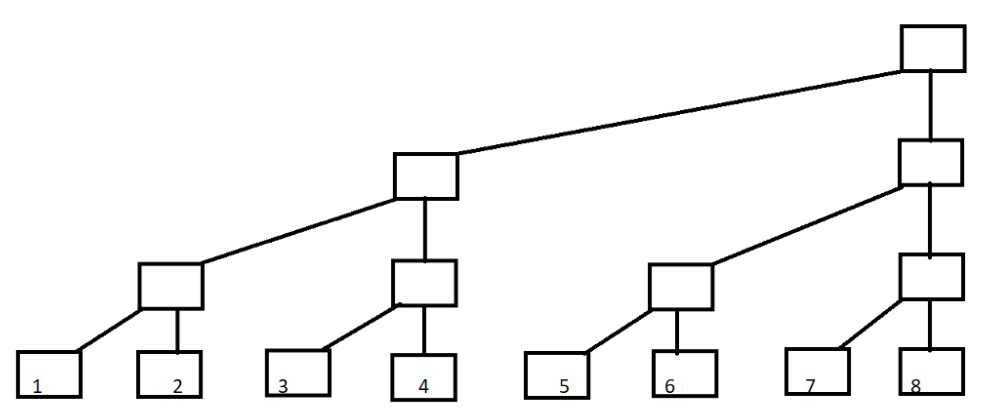
定义每一列的顶端结点C[]数组

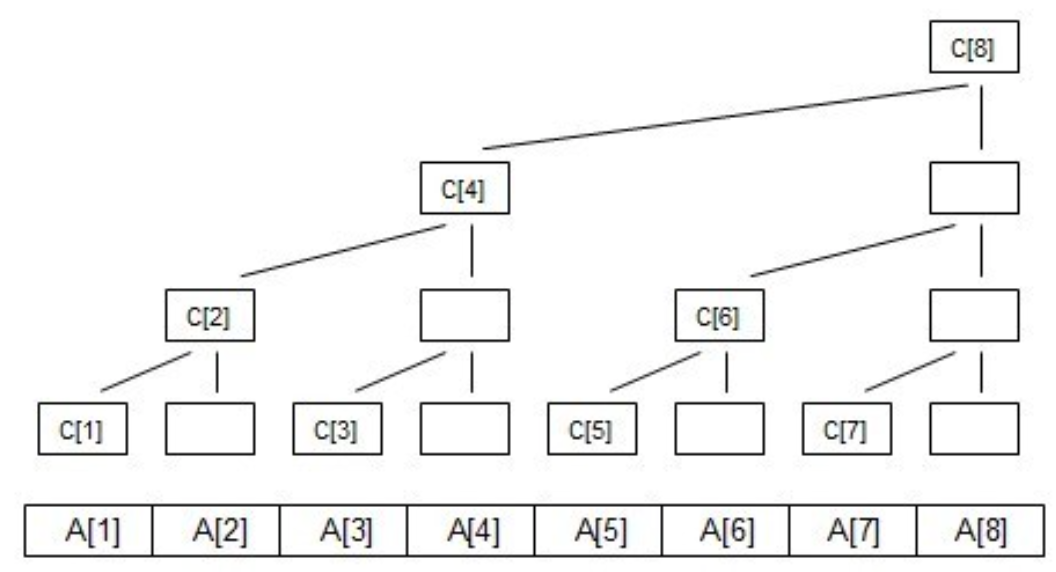
C[i]代表 子树的叶子结点的权值之和

如图可知

1
2
3
4
5
6
7
8

C[1]=A[1];
C[2]=A[1]+A[2]=A[2];
C[3]=A[3];
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
C[6]=A[5]+A[6];
C[7]=A[7];
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

将下标转换为二进制，并转化为递归式：

1
2
3
4
5
6
7
8

C[1]=C[00000001]=A[1];
C[2]=C[00000010]=A[2]+C[1];
C[3]=C[00000011]=A[3];
C[4]=C[00000100]=A[4]+C[3]+C[2];
C[5]=C[00000101]=A[5];
C[6]=C[00000110]=A[6]+C[5];
C[7]=C[00000111]=A[7];
C[8]=C[00001000]=A[8]+C[7]+C[6]+C[4];

树状数组C[]存在如下规律：

• C[i]是A[..i]的部分元素和；

• C[i]和中一定包含A[i];

• C[i]和中一定不包含A[j](j>i);

• $ C[i] = A[i - 2k+1] + A[i - 2k+2] + … + A[i] $

其中：k为i的二进制中从最低位到高位连续零的长度

引入lowbit(x): x & -x , 用于快速计算x的最低位1开始截断的数($lowbit(x) = 2^k$)， 有

1
2
3
4
5
6
7
8

lowbit(1) = lowbit(0000000_1) = 00000001 = 2^0 = 1 (k=0)
lowbit(2) = lowbit(000000_10) = 00000010 = 2^1 = 2 (k=1)
lowbit(3) = lowbit(0000001_1) = 00000001 = 2^0 = 1 (k=0)
lowbit(4) = lowbit(00000_100) = 00000100 = 2^2 = 4 (k=2)
lowbit(5) = lowbit(0000010_1) = 00000001 = 2^0 = 1 (k=0)
lowbit(6) = lowbit(000001_10) = 00000010 = 2^1 = 2 (k=1)
lowbit(7) = lowbit(0000011_1) = 00000001 = 2^0 = 1 (k=0)
lowbit(8) = lowbit(0000_1000) = 00001000 = 2^3 = 8 (k=3)

引入lowbit(x)后，通过lowbit(x)可快速递归计算和x有关的下标，主要有两种：

• 树左侧和C[x]不相连的最近节点，其下标可通过x -= lowbit(x)依次访问， 这些节点不包含重复元素；

• 树右侧和C[x]相连的最近父节点，其下标可通过x += lowbit(x)依次访问，父节点包含了子节点；

借助lowbit(x)的这2种特性，可分别快速树状数组的两种操作流程：

修改操作：modify(i, diff)

• 任一C[i]存储的是从nums[i]开始的部分nums[]和， 所以如果更新nums[i]，则需要更新从C[i]开始到C[n]所有包含nums[i]的相关C[]节点的值;

• 从C[i]开始, 首先更新当前节点C[i]: C[i] += diff;

• 通过 i += lowbit(i)计算上一级的C[i]下标， 更新上一级节点C[i] += diff;

• 直到 i > nums.len(), 更新结束；

查询操作：prefix_sum(i)

• prefix_sum(i)用于计算nums[0..i]前缀和；

• prefix_sum(i)为只和C[i]及前面的C[]有关；

• 初始化累加和prefix_sum = 0;

• 从i开始， 计算累加和prefix_sum += C[i];

• 通过i -= lowbit(i)计算下一个下标，计算累加和prefix_sum += C[i];

• 直到i==0, 查询结束；

• 返回累加和prefix_sum

相关题目

• 307.区域和检索-数组可修改

参考

1. 树状数组彻底入门

2. 树状数组详解