线性代数
一、基本知识
- 本书中所有的向量都是列向量, 形式为:
$$ \overrightarrow{\mathbf{x}} = \left[ \begin{array} {c} {x_{1}} \ {x_{2}} \ {\vdots} \ {x_{n}} \end{array} \right] $$
本书中所有的矩阵$\mathbf{X} \in \mathbb{R}^{m \times n}$都表示为:
$$ \mathbf{X} = \left[ \begin{array} {cccc} {x_{1,1}} & {x_{1,2}} & {\cdots} & {x_{1, n}} \ {x_{2,1}} & {x_{2,2}} & {\cdots} & {x_{2, n}} \ {\vdots} & {\vdots} & {\ddots} & {\vdots} \ {x_{m, 1}} & {x_{m, 2}} & {\cdots} & {x_{m, n}} \end{array} \right] $$
简写为:$\left(x_{i, j}\right)_{m \times n}$ 或者 $\left[x_{i, j}\right]_{m \times n}$ 。
矩阵的范数:设矩阵 $\mathbf{A}=\left(a_{i, j}\right)_{m \times n}$,则其范数$F$为:$|\mathbf{A}|_{F}=\sqrt{\sum_{i, j} a_{i, j}^{2}}$。它是向量的$L_{2}$ 范数的推广。
矩阵的迹:设矩阵$\mathbf{A}=\left(a_{i, j}\right)_{m \times n}$,则$\mathbf{A}$的迹为:$\operatorname{tr}(\mathbf{A})=\sum_{i} a_{i, i}$。
矩阵$\mathbf{A}$的迹性质有:
范数与迹:$|\mathbf{A}|_{F}=\sqrt{\operatorname{tr}\left(\mathbf{A} \mathbf{A}^{T}\right)}$ 。
$\mathbf{A}$的迹等于$\mathbf{A}^{T}$ 的迹:$\operatorname{tr}(\mathbf{A})=\operatorname{tr}\left(\mathbf{A}^{T}\right)$ 。
交换律:假设$\mathbf{A} \in \mathbb{R}^{m \times n}$, $\mathbf{B} \in \mathbb{R}^{n \times m}$则有:$\operatorname{tr}(\mathbf{A} \mathbf{B})=\operatorname{tr}(\mathbf{B} \mathbf{A})$ 。
结合律:$\operatorname{tr}(\mathbf{A B C})=\operatorname{tr}(\mathbf{C A B})=\operatorname{tr}(\mathbf{B C A})$。
二、向量
- 一组向量 $\overrightarrow{\mathbf{v}}{1}, \overrightarrow{\mathbf{v}}{2}, \cdots, \overrightarrow{\mathbf{v}}{n}$ 是线性相关的:指存在一组不全为零的实数$a{1}, a_{2}, \cdots, a_{r}$ ,使得:$\sum_{i=1}^{n} a_{i} \overrightarrow{\mathbf{v}}_{i}=\overrightarrow{\mathbf{0}}$。
一组向量 $\overrightarrow{\mathbf{v}}{1}, \overrightarrow{\mathbf{v}}{2}, \cdots, \overrightarrow{\mathbf{v}}{n}$ 是线性无关的,当且仅当 $a{i}=0, i=1,2, \cdots, n$时,才有:$\sum_{i=1}^{n} a_{i} \overrightarrow{\mathbf{v}}_{i}=\overrightarrow{\mathbf{0}}$
向量空间维数:一个向量空间所包含的最大线性无关向量的数目。
向量的点积:$\overrightarrow{\mathbf{u}} \cdot \overrightarrow{\mathbf{v}}=u_{x} v_{x}+u_{y} v_{y}+u_{z} v_{z}=|\overrightarrow{\mathbf{u}}||\overrightarrow{\mathbf{v}}| \cos (\overrightarrow{\mathbf{u}}, \overrightarrow{\mathbf{v}})$
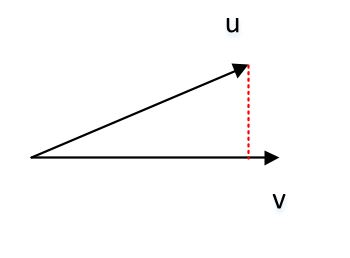
- 三维向量的叉积:
$$ \overrightarrow{\mathbf{w}} =\overrightarrow{\mathbf{u}} \times \overrightarrow{\mathbf{v}} =\left[ \begin{array} {ccc} {\overrightarrow{\mathbf{i}}} & {\overrightarrow{\mathbf{j}}} & {\overrightarrow{\mathbf{k}}} \ {u_{x}} & {u_{y}} & {u_{z}} \ {v_{x}} & {v_{y}} & {v_{z}} \end{array} \right] $$
其中 $\overrightarrow{\mathbf{i}}, \overrightarrow{\mathbf{j}}, \overrightarrow{\mathbf{k}}$分别为 x, y, z 轴的单位向量。
$$ \overrightarrow{\mathbf{u}}=u_{x} \overrightarrow{\mathbf{i}}+u_{y} \overrightarrow{\mathbf{j}}+u_{z} \overrightarrow{\mathbf{k}}, \quad \overrightarrow{\mathbf{v}}=v_{x} \overrightarrow{\mathbf{i}}+v_{y} \overrightarrow{\mathbf{j}}+v_{z} \overrightarrow{\mathbf{k}} $$
- $\overrightarrow{\mathbf{u}}$和 $ \overrightarrow{\mathbf{v}}$ 的叉积垂直于 $\overrightarrow{\mathbf{u}}, \overrightarrow{\mathbf{v}}$构成的平面,其方向符合右手规则。
- 叉积的模等于$\overrightarrow{\mathbf{u}}, \overrightarrow{\mathbf{v}}$ 构成的平行四边形的面积。
- $\overrightarrow{\mathbf{u}} \times \overrightarrow{\mathbf{v}}=-\overrightarrow{\mathbf{v}} \times \overrightarrow{\mathbf{u}}$。
- $\overrightarrow{\mathbf{u}} \times(\overrightarrow{\mathbf{v}} \times \overrightarrow{\mathbf{w}})=(\overrightarrow{\mathbf{u}} \cdot \overrightarrow{\mathbf{w}}) \overrightarrow{\mathbf{v}}-(\overrightarrow{\mathbf{u}} \cdot \overrightarrow{\mathbf{v}}) \overrightarrow{\mathbf{w}}$。
- 三维向量的混合积:
- 其物理意义为:以 为三个棱边所围成的平行六面体的体积。 当 构成右手系时,该平行六面体的体积为正号。
- 两个向量的并矢:给定两个向量 ,则向量的并矢记作:
也记作 或者
三、矩阵
- 给定两个矩阵 ,定义:
- 阿达马积
Hadamard product(又称作逐元素积): - 克罗内积
Kronnecker product:
- 设 为 阶向量, 为 阶方阵,则:
如果 是一元函数,则:
- 其逐元向量函数为:
- 其逐矩阵函数为:
- 其逐元导数分别为:
各种类型的偏导数:
- 标量对标量的偏导数
- 标量对向量( 维向量)的偏导数
- 标量对矩阵( 阶矩阵)的偏导数
- 向量( 维向量)对标量的偏导数
向量( 维向量)对向量 ( 维向量) 的偏导数(雅可比矩阵,行优先)
如果为列优先,则为上面矩阵的转置
- 矩阵( 阶矩阵)对标量的偏导数
更复杂的情况依次类推。对于 。根据
numpy的术语:- 假设 的
ndim(维度)为
对于标量,
ndim为 0;对于向量,ndim为 1;对于矩阵,ndim为 2- 假设 的
ndim为
- 则 的
ndim为 - 矩阵($m \times n$ 阶矩阵)对标量的偏导数
- 假设 的
$$ \frac{\partial \mathbf{U}}{\partial v} =\left[ \begin{array} {cccc} {\frac{\partial U_{1,1}}{\partial v}} & {\frac{\partial U_{1,2}}{\partial v}} & {\cdots} & {\frac{\partial U_{1, n}}{\partial v}} \ {\frac{\partial U_{2,1}}{\partial v}} & {\frac{\partial U_{2,2}}{\partial v}} & {\cdots} & {\frac{\partial U_{2, n}}{\partial v}} \ {\vdots} & {\vdots} & {\ddots} & {\vdots} \ {\frac{\partial U_{m, 1}}{\partial v}} & {\frac{\partial U_{m, 2}}{\partial v}} & {\cdots} & {\frac{\partial U_{m, n}}{\partial v}} \end{array} \right] $$
- 对于矩阵的迹,有下列偏导数成立:
$$ \frac{\partial[\operatorname{tr}(f(\mathbf{X}))]}{\partial \mathbf{X}} =\left(f^{\prime}(\mathbf{X})\right)^{T} $$
$$ \frac{\partial[\operatorname{tr}(\mathbf{A} \mathbf{X} \mathbf{B})]}{\partial \mathbf{X}} =\mathbf{A}^{T} \mathbf{B}^{T} $$
$$ \frac{\partial\left[\operatorname{tr}\left(\mathbf{A} \mathbf{X}^{T} \mathbf{B}\right)\right]}{\partial \mathbf{X}}=\mathbf{B} \mathbf{A} $$
$$ \frac{\partial[\operatorname{tr}(\mathbf{A} \otimes \mathbf{X})]}{\partial \mathbf{X}}=\operatorname{tr}(\mathbf{A}) \mathbf{I} $$
$$ \frac{\partial[\operatorname{tr}(\mathbf{A} \mathbf{X B} \mathbf{X})]}{\partial \mathbf{X}}=\mathbf{A}^{T} \mathbf{X}^{T} \mathbf{B}^{T}+\mathbf{B}^{T} \mathbf{X} \mathbf{A}^{T} $$
$$ \frac{\partial\left[\operatorname{tr}\left(\mathbf{X}^{T} \mathbf{B} \mathbf{X} \mathbf{C}\right)\right]}{\partial \mathbf{X}}=\mathbf{B} \mathbf{X} \mathbf{C}+\mathbf{B}^{T} \mathbf{X} \mathbf{C}^{T} $$
$$ \frac{\partial\left[\operatorname{tr}\left(\mathbf{C}^{T} \mathbf{X}^{T} \mathbf{B} \mathbf{X} \mathbf{C}\right)\right]}{\partial \mathbf{X}}=\left(\mathbf{B}^{T}+\mathbf{B}\right) \mathbf{X} \mathbf{C} \mathbf{C}^{T} $$
$$ \frac{\partial\left[\operatorname{tr}\left(\mathbf{A} \mathbf{X} \mathbf{B} \mathbf{X}^{T} \mathbf{C}\right)\right]}{\partial \mathbf{X}}=\mathbf{A}^{T} \mathbf{C}^{T} \mathbf{X} \mathbf{B}^{T}+\mathbf{C} \mathbf{A} \mathbf{X} \mathbf{B} $$
$$ \frac{\partial[\operatorname{tr}((\mathbf{A} \mathbf{X B}+\mathbf{C})(\mathbf{A} \mathbf{X B}+\mathbf{C}))]}{\partial \mathbf{X}}=2 \mathbf{A}^{T}(\mathbf{A} \mathbf{X B}+\mathbf{C}) \mathbf{B}^{T} $$
- 假设$\mathbf{U}=f(\mathbf{X})$是关于 $\mathbb{X}$ 的矩阵值函数$\left(f : \mathbb{R}^{m \times n} \rightarrow \mathbb{R}^{m \times n}\right)$,且 是关于 的实值函数$\left(g : \mathbb{R}^{m \times n} \rightarrow \mathbb{R}\right)$,则下面链式法则成立:
$$
\begin{aligned}
\frac{\partial g(\mathbf{U})}{\partial \mathbf{X}}
= \left(
\frac{\partial g(\mathbf{U})}{\partial x_{i, j}}
\right)
=&\left[
\begin{array}
{ccc}
{\frac{\partial g(\mathbf{U})}{\partial x_{1,1}}} &
{\frac{\partial g(\mathbf{U})}{\partial x_{1,2}}} &
{\cdots} &
{\frac{\partial g(\mathbf{U})}{\partial x_{1, n}}} \
{\frac{\partial g(\mathbf{U})}{\partial x_{2,1}}} &
{\frac{\partial g(\mathbf{U})}{\partial x_{2,2}}} &
{\cdots} &
{\frac{\partial g(\mathbf{U})}{\partial x_{2, n}}} \
{\vdots} & {\vdots} & {\ddots} & {\vdots} \
{\frac{\partial g(\mathbf{U})}{\partial x_{m, 1}}} &
{\frac{\partial g(\mathbf{U})}{\partial x_{m, 2}}} &
{\cdots} &
{\frac{\partial g(\mathbf{U})}{\partial x_{m, n}}}
\end{array}
\right] \
&=\left(
\sum_{k}
\sum_{l}
\frac{\partial g(\mathbf{U})}{\partial u_{k, l}}
\frac{\partial u_{k, l}}{\partial x_{i, j}}
\right) \
&=\operatorname{tr}
\left[
\left(
\frac{\partial g(\mathbf{U})}{\partial \mathbf{U}}
\right)^{T}
\frac{\partial \mathbf{U}}{\partial x_{i, j}}
\right]
\end{aligned}
$$