梯度下降算法 转载

设一个简单的函数 $ 𝑦 = f(x) = 3𝑥^2+2𝑥+1 $。假设此时𝑥=10，那么𝑦=321，

想要求取这个函数的最值, 一般可以对 f(x) 求导: f'(x) = 0 来得到.

可以求出目标函数的导函数为：$ 𝑦′= 6𝑥+2 $。

但现实中的函数维度极度复杂, 在复杂的函数空间内可能求不出来极小值点。

即利用梯度下降的方式来求得𝑦的最小值和对应的𝑥的值。

万事具备，再来回顾下导数的意义：

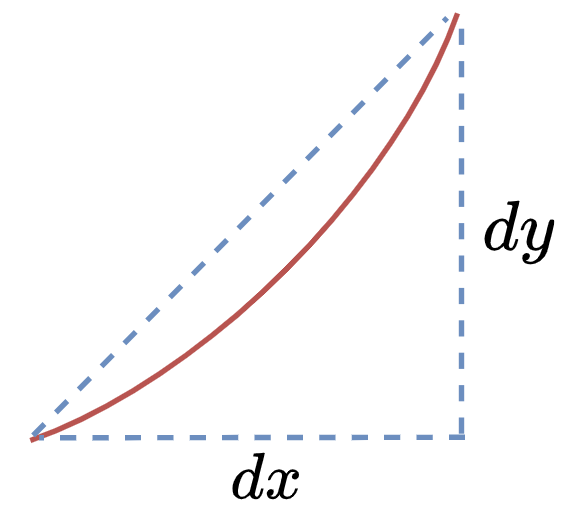
无限放大曲线的一小部分，在𝑦轴方向截取一段𝑑𝑦，向𝑥轴方向截取一段𝑑𝑥，

则$ 𝑓′(𝑥)=\frac{𝑑𝑦}{𝑑𝑥} $即为这一小段曲线的斜率，也为导数值。

当然，具体到实际问题，并不是取一段曲线而是以一个具体的点计算，这里只是距离。

如 $ 𝑓(𝑥)=2𝑥^2 $ 在 𝑥=2 处的导数值为8。

梯度的本意是一个向量（矢量），即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大，显而易见，对一元函数而言就是求导(多元函数求偏导并含有方向)。

继续推导，可以得到这样的式子：$ 𝑓′(𝑥)𝑑𝑥=𝑑𝑦 $。

在详细一点，当前𝑥=10，我们取一个固定的𝑑𝑥=0.2，沿着导数的方向，让𝑥逐渐的变化，此时的𝑦也逐渐变小，是不是就能逐步得到目标函数的最小值呢？

数学语言如下：

初始化𝑥
开始迭代：
- 求𝑓(𝑥)的导数𝑓′(𝑥)
- $ 𝑥_{𝑖 + 1} = 𝑥_𝑖 − 𝑑𝑥∗𝑓′(𝑥) $
- 𝑖++

即迭代示意图如下：

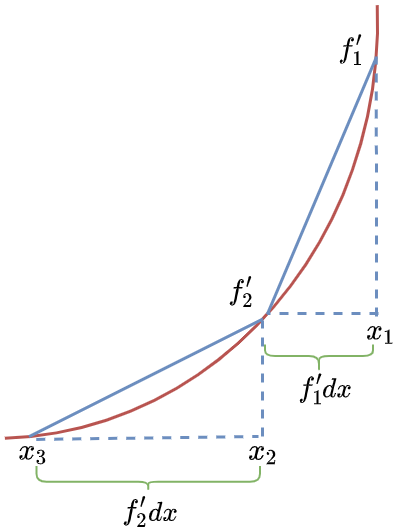
$ 𝑥_1 − 𝑓_1′𝑑𝑥=𝑥_2 $，$ 𝑓_1′ $为$ 𝑥_1 $处的导数值
$ 𝑥_2−𝑓_2′𝑑𝑥=𝑥_3 $，$ 𝑓_2′ $为$ 𝑥_2 $处的导数值

将𝑑𝑥换成𝛼，含义为学习率，即每次行走的步幅, 直到行走到最低点结束，代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
dx = 0.2
n_eproch = 1000
x = -10 
ls = []

for _ in range(n_eproch):  
    y = 3 * x ** 2 + 2 * x + 1
    ls.append(y)
    x = x - (6 * x + 2) * dx

print(ls[-1])
# 0.67

可见在迭代1000次后，𝑦的最终取值为0.67，和函数实际的最小值不谋而合，这就是梯度下降的力量。

对于复杂的多元函数求偏导，或者求导的链式法则，还是借助Tensorflow这种专业工具更加省事。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
import tensorflow as tf

X = tf.constant([0., 0.25, 0.5, 0.74, 1.])
y = tf.constant([0., 0.36, 0.54, 0.82, 1.])

a = tf.Variable(initial_value=0.)
b = tf.Variable(initial_value=0.)
variables = [a, b]

num_epoch = 100
optimizer = tf.keras.optimizers.SGD(learning_rate=5e-4)
for e in range(num_epoch):
    # 使用tf.GradientTape()记录损失函数的梯度信息
    with tf.GradientTape() as tape:
        y_pred = a * X + b
        loss = tf.reduce_sum(tf.square(y_pred - y))
    # TensorFlow自动计算损失函数关于自变量（模型参数）的梯度
    grads = tape.gradient(loss, variables)
    # TensorFlow自动根据梯度更新参数
    optimizer.apply_gradients(grads_and_vars=zip(grads, variables))

print(a, b)

反向传播

反向传播是一种以梯度下降为基础，对误差进行反馈，并调节相关参数的方法.

以MLP为例，首先构建结构如下图所示的网络：

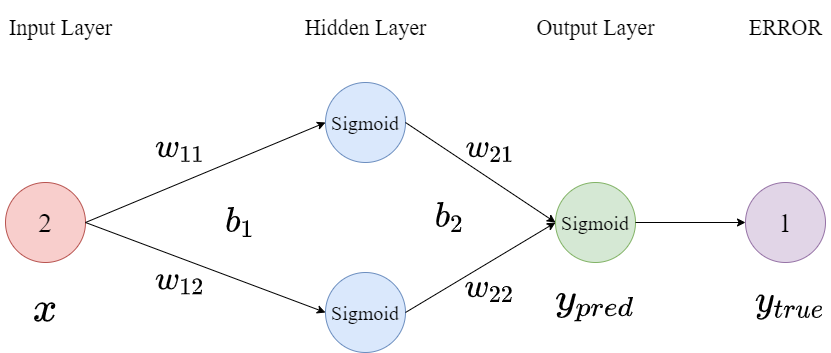
然后完成参数的初始化，且激活函数均采用Sigmoid: $ 𝑓(𝑥)=\frac{1}{1+𝑒^{−𝑥}}$

初始参数如下: $ 𝑥=2,𝑤_{11}=1,𝑤_{12}=−1,𝑏_1=3,𝑤_{21}=2,𝑤_{22}=1,𝑏_2=0,𝑦_{𝑡𝑟𝑢𝑒}=1,𝛼=0.2 $

前向计算

隐藏层第一个神经元：$ 𝑥 * 𝑤_{11}+𝑏_1=5 $，激活后的输出为: $ \frac{1}{1+e^{-5}} = 0.99 $
隐藏层第二个神经元：$ 𝑥 * 𝑤_{12}+𝑏_1=1 $，激活后的输出为: $ \frac{1}{1+e^{-1}} = 0.73 $
输出层的预测输出为：$ 𝑦_{𝑡𝑒𝑚𝑝} = 0.99 * 𝑤_{21}+0.73 * 𝑤_{22}+𝑏_2=2.71 $，激活后的输出为: $ y_{pred} =\frac{1}{1 + e^{-2.71}} = 0.93 $
计算Loss：$ 𝐸 = \frac{1}{2}(𝑦_{𝑡𝑟𝑢𝑒}−𝑦_{𝑝𝑟𝑒𝑑})^2 $ (均方误差, 选用这类型是是因为求导方便，绝对值函数不一定可导)

反向传播

补充一下对Sigmoid函数求导的结果为：$ {\frac{1}{1+𝑒^{−𝑥}}}′=\frac{𝑒^𝑥}{𝑒^{2𝑥}+2𝑒^𝑥+1} $
𝐸对输出层求导：$ \frac{𝜕𝐸}{𝜕𝑦_{𝑝𝑟𝑒𝑑}} = \frac{𝜕({\frac{1}{2} (y_{true} - y_{pred})^2})}{𝜕y_{pred}} = 𝑦_{𝑝𝑟𝑒𝑑}−𝑦_{𝑡𝑟𝑢𝑒} = 0.93 - 1 = −0.07 $
而$ 𝑦_{𝑝𝑟𝑒𝑑}=Sigmoid(𝑦_{𝑡𝑒𝑚𝑝})，\frac{𝜕𝑦_{𝑝𝑟𝑒𝑑}}{𝜕𝑦_{𝑡𝑒𝑚𝑝}}=\frac{𝑒^{2.71}}{𝑒^{5.42}+2𝑒^{2.71}+1}=0.058 $
而计算$ 𝑦_{𝑡𝑒𝑚𝑝} $对$ 𝑤_{21}$ 这个参数的偏导值：$ \frac{𝜕𝑦_{𝑡𝑒𝑚𝑝}}{𝜕𝑤_{21}} = \frac{𝜕(0.99*𝑤_{21} + 0.73*𝑤_{22} + 𝑏_2)}{𝜕𝑤_{21}} = 0.99 $ (求偏导时无关变量视为常量)
通过链式法则求误差𝐸对参数𝑤21的梯度：$ \frac{𝜕𝐸}{𝜕𝑤_{21}} = \frac{𝜕𝐸}{𝜕𝑦_{𝑝𝑟𝑒𝑑}}× \frac{𝜕𝑦_{𝑝𝑟𝑒𝑑}}{𝜕𝑦_{𝑡𝑒𝑚𝑝}} × \frac{𝜕𝑦_{𝑡𝑒𝑚𝑝}}{𝜕𝑤_{21}} = −0.004 $
𝑤21沿着梯度下降即可：$ 𝑤_{21}' = 𝑤_{21} + 𝛼 × −0.004 = 2+0.2×−0.004=1.9992 $，这样，参数𝑤21就得到了更新。(同上文的梯度下降方法)

以此类推，通过不断的迭代，参数会逐渐修改，最终的结果是模型能有效的对输入进行预测或者分类。其他参数的更新同理。对于经常编程的小伙伴，会发现训练过程经常使用batch，此时最终的误差为这个bacth的总误差，需要对总误差求均值或求和等操作：

1
2
loss = tf.keras.losses.sparse_categorical_crossentropy(y_true=y, y_pred=y_pred)
loss = tf.reduce_mean(loss)

参考

https://muyuuuu.github.io/2020/05/09/back-propagation-and-gradient-descent/

梯度下降算法转载

梯度下降算法转载

反向传播

前向计算

反向传播

参考

相关文章：