MassTree

简介

masstree 来源于 2012 年发表的论文(Cache craftiness for fast multicore key-value storage)，可以理解为 B+ Tree 和 Radix Tree 的混合体，即将键切分成多个部分，每个部分为一个节点；每个节点内部又是一个 B+ Tree，兼顾空间和性能。

特点

Masstree 将变长键划分成多个固长部分，每个固长部分可以通过 int 类型表示，而不是 char 类型。由于处理器处理 int 类型比较操作的速度远远快于 char 数组的比较，因此 Masstree 通过 int 类型的比较进一步加速了查找过程。固定长度可以设置为 CPU 缓存行长度，以增加 CPU 缓存效率。
每个节点是一个 B+ Tree，因此 CPU 在查询的时候可以将节点所代表的 B+ Tree 加载到 CPU 缓存中，以增加 CPU 缓存命中率。
其并发控制用到了 Read-Copy-Update(RCU)。读不因任何数据更新而阻塞，但更新数据的时候，需要先复制一份副本，在副本上完成修改，再一次性地替换旧数据。因此读不会造成 CPU 缓存无效。

结构

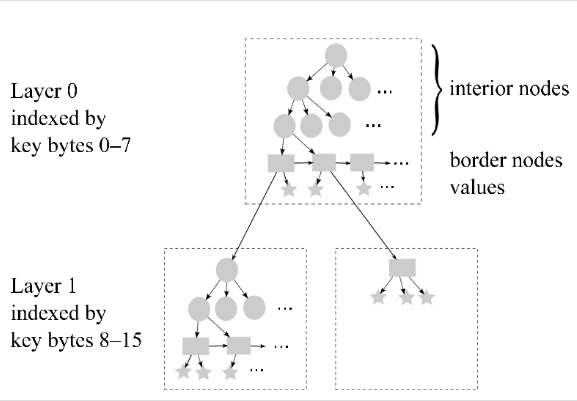
Mass Tree 算法

并发策略

Mass Tree 的并发策略和 OLFIT Tree 是相似的：

fine-grained locking，即节点锁，解决 write-write 竞争，同一时刻只有一个线程可以对当前节点进行写操作
optimistic concurrency control，即节点 version (uint32_t)，解决 read-write 竞争，读开始前和读结束后都需要获取当前节点的最新 version，来判断在读过程中当前节点是否发生了写操作（插入或分裂），同时对节点的写操作都需要先修改 version，在插入 key 之前需要设置 inserting 标记，插入完成之后将 insert 的 vinsert + 1；在分裂之前需要设置 splitting 标记，分裂完成之后将 split 的 vsplit + 1。

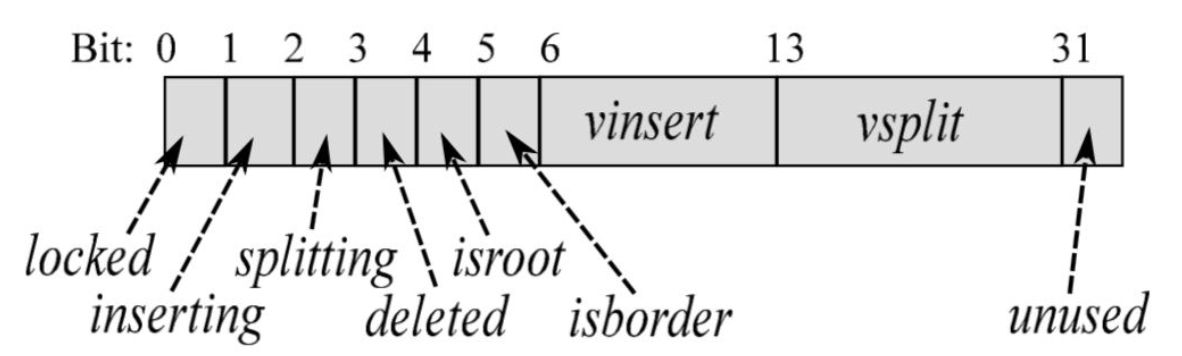
和 permutation 一样，version 也被划分成了多个域，除了带有 insert 和 split 信息之外，还包含一个 lock bit，用于加锁；一个 root bit，用于指示否是根节点；一个 border bit，用于指示是否是 border node；一位 deleted 位，用于指示这个节点是否被标记为删除。

下降流程

对于每次插入，获取，删除操作，都需要从 root（可能是整棵树的根节点，也可能是某棵子树的根节点）下降到对应的叶节点（border node）。

首先，在开始读取节点之前，必须获得节点的 stable version（图中橙色方块），即 version 中的 inserting 和 splitting 位都为 0。

其次，在下降之前，需要获取最新的 root，因为在开始下降前，根节点可能分裂了，导致其发生了改变（图中蓝色方块）。

最后，如果当前节点已经是叶节点，那么可以返回，否则需要进行下降，读取内部结点根据 key[x, x+8)(8 字节) 获得下降节点之后，分为 3 种情况处理：

case 1 那行伪代码可以这样用 C 语言表示：

1
2
3
4
5
uint32_t before = node_get_stable_version(n);
// read node here
uint32_t after = node_get_version(n); // no need to be stable, just latest version
if ((before ^ after == LOCK_BIT) || (before ^ after == 0))
    // neither insert nor split happened

节点在我们读取期间没有发生任何变化，我们可以安全地进行下降；

节点发生了变化，而且是分裂，那么我们需要从根节点重新进行下降（内部节点没有相互连接起来，所以不能像 Blink Tree 那样获取右节点）；
节点发生了变化，但只是插入，只需要重新对当前节点进行下降

注意第二个黄色方块，这一行非常关键，如果你细看下的话，它似乎可以挪到 case 1 的 if 语句里面，但实际上不能这样做。因为如果当前节点的孩子节点发生了分裂，但是还没来得及将新节点插入到当前节点，对调这两行代码，可能会导致下降到错误的节点。

插入流程

作者只给出了读取伪代码，这里给出插入伪代码。

当我们通过 findborder 下降到叶节点后，需要对其加锁（图中蓝色方块），但是此时并不能直接将 key 进行插入，当两个写线程同时下降到同一个叶节点时，只有一个线程可以进行写入，所以加锁后需要查看在加锁前是否有其他线程对这个节点进行了写入，如果有的话需要查看是否需要右移，这里的逻辑和 Blink Tree 是一样的。

当我们成功加锁并且定位到正确的叶节点之后，可以进行写入，结果有 4 种：

插入 key 成功或 key 已经存在；
需要下降到下一层，同时需要增加索引的偏移；
存在索引冲突，比如 "12345678AA" 和 "12345678BB"，此时需要创建一棵子树，存放 "AA" 和 "BB"，同时需要把原来存放 "AA" 的地方替换成这棵子树的根节点
节点已满，需要分裂之后再次插入（见下一小节）

橙色方块在下面删除流程中介绍

实现

UncP/aili，没有实现删除操作；
https://github.com/rmind/masstree，采用了激进生成子树的策略，缺点就是 cache locality 在有些情况下不好。
论文作者的实现：https://github.com/kohler/masstree-beta。

总结

Trie 和 B+ 两种索引树的结合，使得在下降过程中的重试不需要从整棵树的根节点开始，同时加快拥有相同前缀的 key 的处理速度
具体的内部结点与外部节点的结构
fine-grained locking 写以及 lock-free 读
比较具体的节点删除机制
较小的节点减少了线程的竞争

需要指出的是这个算法不支持性能线性扩展，不过这并不是问题。

这个算法实现起来很有挑战性，个人认为主要有两个方面，第一个是对于树结构的把握，Mass Tree 是 Trie 和 B+ 树的结合。第二个是对于并发下可见性的理解，”先改哪个域后改哪个域“，”谁先可见谁后可见“，”谁何时可见“，“在哪加以及加不加 memory barrier”等等这样的问题需要花很多时间考虑，而且出现 bug 非常难调试。

Mass Tree 性能比我预想中要好很多，对于均匀分布的 10 字节 key 随机插入，数据量 1000 万，在我的机器上 4 个线程可以到 500 万以上的 tps；对于分布集中的测试数据，可以到 1000 万以上。其实对于内存索引来说，cache miss 对性能造成的影响有时候是远远大于线程竞争的，所以尽管数据分布非常集中（线程竞争更多），仍然可以获得更高的性能。

MassTree

相关文章：