B-Tree, B+Tree, B*Tree
B树(B-Tree)
B-Tree是1972年由Rudolf Bayer和Ed M. McCreight在Boeing Research Labs发明的一种数据结构;B-Tree是为磁盘等外存储设备设计的一种平衡多路查找树(Balance Multiple Search Tree);B-Tree不是二叉树(Binary-Tree), 是一种多叉树;
B树的定义
Knuth 的定义,一个 m 阶的B树是一个有以下属性的树:
- 每一个节点最多有 m 个子节点;
- 每一个非叶子节点(除根节点)最少有 ⌈m/2⌉ 个子节点
- 如果根节点不是叶子节点,那么它至少有两个子节点
- 有 k 个子节点的非叶子节点拥有 k − 1 个键
- 所有的叶子节点都在同一层;
B树特点
B树的每个节点同时包含(K,V);
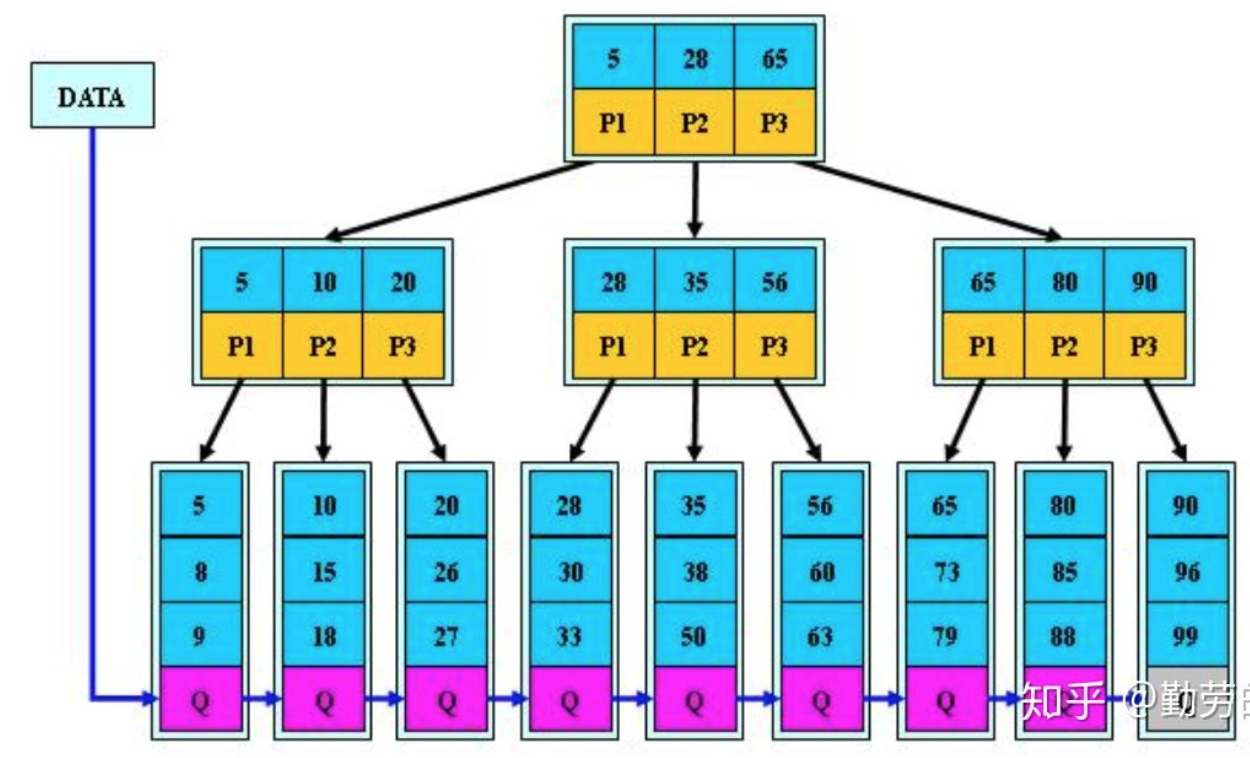
B树的操作
查找
来模拟下查找文件 29 的过程:
(1) 根据根结点指针找到文件目录的根磁盘块 1,将其中的信息导入内存。【磁盘 IO 操作 1 次】
(2) 此时内存中有两个文件名 17,35 和三个存储其他磁盘页面地址的数据。根据算法我们发现 17<29<35,因此我们找到指针 p2。
(3) 根据 p2 指针,我们定位到磁盘块 3,并将其中的信息导入内存。【磁盘 IO 操作 2 次】
(4) 此时内存中有两个文件名 26,30 和三个存储其他磁盘页面地址的数据。根据算法我们发现 26<29<30,因此我们找到指针 p2。
(5) 根据 p2 指针,我们定位到磁盘块 8,并将其中的信息导入内存。【磁盘 IO 操作 3 次】
(6) 此时内存中有两个文件名 28,29。根据算法我们查找到文件 29,并定位了该文件内存的磁盘地址。
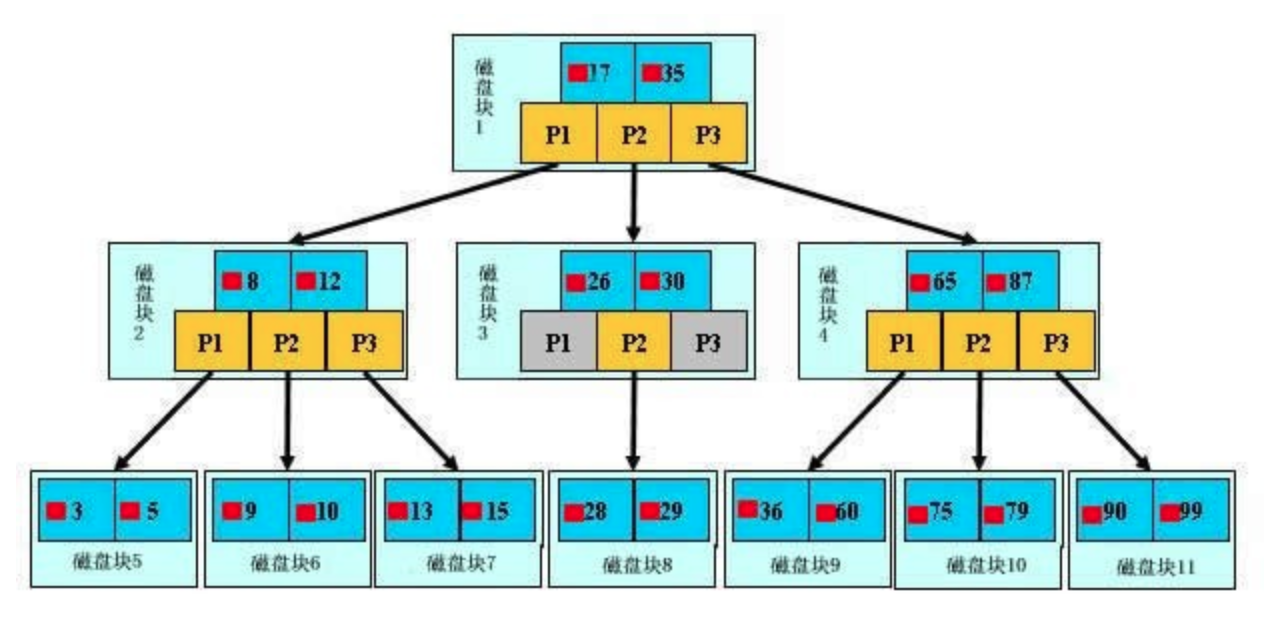
插入
针对m阶高度h的B树,插入一个元素时,首先在B树中是否存在,如果不存在,即在叶子结点处结束,然后在叶子结点中插入该新的元素。
- 若该节点元素个数小于m-1,直接插入;
- 若该节点元素个数等于m-1,引起节点分裂;以该节点中间元素为分界,取中间元素(偶数个数,中间两个随机选取)插入到父节点中;
- 重复上面动作,直到所有节点符合B树的规则;最坏的情况一直分裂到根节点,生成新的根节点,高度增加1;
上面三段话为插入动作的核心;
删除
首先查找B树中需删除的元素, 如果该元素在B树中存在,则将该元素在其结点中进行删除;
删除该元素后,首先判断该元素是否有左右孩子结点,
如果有,则上移孩子结点中的某相近元素(“左孩子最右边的节点”或“右孩子最左边的节点”)到父节点中,然后是移动之后的情况;
如果没有,直接删除。
- 某结点中元素数目小于(m/2)-1,(m/2)向上取整,则需要看其某相邻兄弟结点是否丰满;
- 如果丰满(结点中元素个数大于(m/2)-1),则向父节点借一个元素来满足条件;
- 如果其相邻兄弟都不丰满,即其结点数目等于(m/2)-1,则该结点与其相邻的某一兄弟结点进行“合并”成一个结点;
B+树(B+Tree)
B+树是B-Tree的一种变种,使其更适合实现外存储索引结构;B+树的非叶子节点只包含K, 不包含V,V都位于叶子节点内;B+树的叶子节点按序包含了向后的指针,形成了一个链表,便于范围遍历操作;- MySQL的InnoDB存储引擎和Mongodb就是用
B+Tree实现其索引结构;
特点
B+树的层级更少:相较于B树B+每个非叶子节点存储的关键字数更多,树的层级更少所以查询数据更快;
B+树查询速度更稳定:B+所有关键字数据地址都存在叶子节点上,所以每次查找的次数都相同所以查询速度要比B树更稳定;
B+树天然具备排序功能:B+树所有的叶子节点数据构成了一个有序链表,在查询大小区间的数据时候更方便,数据紧密性很高,缓存的命中率也会比B树高。
B+树全节点遍历更快:B+树遍历整棵树只需要遍历所有的叶子节点即可,而不需要像B树一样需要对每一层进行遍历,这有利于数据库做全表扫描。
B树相对于B+树的优点是:如果经常访问的数据离根节点很近,而B树的非叶子节点本身存有关键字其数据的地址,所以这种数据检索的时候会要比B+树快。
B+树通常用于数据库和操作系统的文件系统中;
插入
删除
B* Tree
B*树是B+树的变种,
相对于B+树他们的不同之处如下:
(1)首先是关键字个数限制问题,B+树初始化的关键字初始化个数是cei(m/2),B*树的初始化个数为(cei(2/3*m))
(2)B+树节点满时就会分裂,而B*树节点满时会检查兄弟节点是否满(因为每个节点都有指向兄弟的指针),如果兄弟节点未满则向兄弟节点转移key,如果兄弟节点已满,则从当前节点和兄弟节点各拿出1/3的数据创建一个新的节点出来;