04.关于数学和人文社科关系的讨论
在第2、3章中,我们在用数学工具定义“权力”、“民智”等概念后,通过数学建模的方式,证明了“民智未开时,适当的权威有助于保障民众的自由”和“随着民智的逐渐开化,降低权威才能最大限度保障民众的自由”这两个重要结论。
但与此同时,这个模型还有很多待完善之处,有些问题甚至会涉及到“数学在人文社科中能够发挥多大作用”这个回答起来并不是那么容易的问题。
作为本专栏的收尾,第4章将对2、3章的模型未来可能的拓展方向进行讨论,并在由此引发的关于“数学在人文社科中扮演的角色”这个问题,进行深度的讨论
一、关于本模型未来可能的发展方向
1、设置目标函数
读过前三章的朋友可能会发现,我在文中并没有针对“制度设计的目的是什么”这个问题进行回答。在第1章中,我举的几个例子蕴含了功利主义的倾向,即以最大化全社会自由之和作为追求目标。而在第3章中,我又表现出了一定的罗尔斯主义的倾向:以弱势者的自由作为评价权力分配格局的标准。
事实上,在整个政治哲学界,也存在着多种目标导向的社会福利函数形式,每种形式都各有利弊,他们大体可被分为以下两类:
可加性社会福利函数,即以最大化 $W=U_{1}+U_{2}+…+U_{i}$ 为目标的社会福利函数。这就是典型的功利主义:追求社会整体自由之和的最大化。它的缺点也很明显:没有考虑贫富差距,允许在某一社会成员的自由度是负数的时候取得最大值。如果行动者A是一个虐待狂,可加性社会福利函数允许A通过虐待B使得B获得负的自由度时,达到社会整体自由度W的最大化。对于可加性社会福利函数的公理化证明、拓展形式及有效性的讨论,详见豪尔绍尼(1955[1]、1975[2])、黄有光(1975[3]、1984[4])
可乘性社会福利函数,即以最大化 $W=U_{1}\cdot U_{2}\cdot …\cdot U_{i} $为目标的社会福利函数。这种社会福利函数的优点在于考虑了贫富差距:弱势者自由度减半必须靠强势者自由度加倍才能弥补,而就绝对值而言前者远远小于后者,这意味着弱势者轻微的损失都会对总社会福利W产生巨大的影响。但它的缺点在于有时候并不如可加性社会福利函数对现实的解释力度更大:如果贫富差距悬殊,弱势者自由度减1可能需要强势者自由度再增加10000才能维持正义性,这很多时候不符合直觉。对于可乘性社会福利函数的公理化证明、拓展形式和有效性的讨论,详见卢斯和拉法(1957[5])、德梅耶和普洛特(1971[6])、金子和中村(1979[7])
本专栏提出的权力-自由模型,亦可以在未来的发展中,加入对目标函数的考量,从而更具有指导实践的价值。至于是选取哪种形式的目标函数,抑或创造新的形式的目标函数,可在未来根据需要进行具体分析。
2、更复杂但贴近现实的收益函数
如第2、3章所展示的那样,本专栏提出的权力-自由模型采取的收益函数$U_{A}=(-a(x+y)+b)x$,是较为初级的线性函数:不仅“价格”部分 $p=-a(x+y)+b$ 是简单线性模型的形式,行动者A的收益也被简单地表示为线性的$ U_{A}=px$ 。
但是,行为经济学家们早已通过对人心理活动的考察,论证了现实中的收益函数不可能是简单的线性函数:它更有可能是非线性的,甚至是不平滑的。典型的例子就是卡尼曼-特沃斯基价值函数(Kahneman-Tversky Value Function)[8]。在这个函数中,收益曲线呈现出一个S型,表明收益呈现出边际效用递减的特点,而这无疑更符合实际:试想,你的总资产只有10万元,和总资产有1000万元的时候,再增加10万元的资产,对你自由度(满足度的数学期望,详见第1章的定义)的提升程度一定是不一样的。
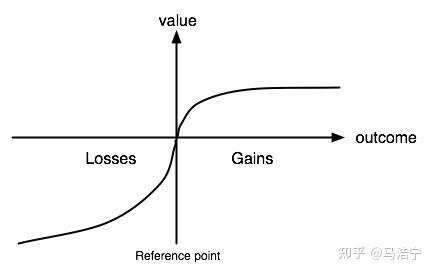
卡尼曼价值函数:效用不是线性的而是边际递减的
因此,本专栏提出的权力-自由模型,可以在未来,结合对人的心理行为的考察,采取更符合现实的收益函数,提升模型的有效性。
3、更多的行动者
在第2、3章的模型中,行动者被笼统地区分为“强势者”和“弱势者”两方。但在现实中,采取一致行动的社会集体存在很多个,至少存在很多诸如“多个弱势方通过结社联合对抗强势方”、“权力不强不弱的中间方游离于强势方和弱势方中间”等多个行动者的可能。
在现代微观经济学中,可以通过博弈论模型,来研究不同情况之下多方博弈的结果:包括多方静态博弈、动态博弈、不完全信息博弈,等等。这些模型已经涵盖了多回合较量、非理性乃至不确定对方是否理性等多种情况,具有很高的参考价值。
本专栏的权力-自由模型,亦可以在未来,通过借鉴博弈论等理论模型,讨论将社会划分为多个行动团体的情况下,权力格局如何设计才最为合理。
4、引入随时间变化的变量
在第3章的最后一节中,通过假定“民智随着时间的推移逐渐开化”,得出了“对强势方的权力制衡应逐渐增大”的结论。
但是,仔细回顾第3章对“民智”的定义,可以看出,这个模型中的“民智”本质上是“民众对事物观测的偏离程度”。但现实中,这种偏离不一定是民众的思考能力差导致的,还有可能是环境的变化,造成先前的生活经验不适用导致的。远的如明朝末年白银的流入,使得中国历史上第一次面临通货紧缩的问题;近的如新冠疫情,导致人类第一次在拥有成熟的生物学和公共卫生学知识的情况下直面高传染性和致病性的病原体。这些例子都表明,按第3章的定义,“民智”乃至强势方的“官智”,都可能不是随时间逐渐升高的。
在这种前提下,就必须重新考虑模型中各变量与时间的关系。例如,“民智” t 或许不是像第3章所展示的那样随时间的推移逐渐提高,而更可能是个周期函数:每发生一次环境变化,就会开启一轮由低到高的循环。而权力制衡系数 k 则又很难配合 t 成为周期函数,否则会面临着一次次“开历史倒车”的质疑:凭什么对权力的制衡一会儿低一会儿高的?该低该高究竟谁说了算?在这种条件下,又该如何设计权力分配格局?这是未来的权力-自由模型,所需要探讨的问题。
在引入随时间变化的变量后,就可以将整个社会的自由的分布视为一个动态的系统。之后,可以通过解关于时间的微分方程、分析李普雅诺夫稳定性等手段,用控制论的方法分析这个动态系统随时间推移的发展方向,进而分析怎样的权力分配才能让系统收敛于最大程度保障自由的状态。
以上分析出了本专栏的权力-自由模型在未来可能的4种发展方向,但到此为止并没有结束。因为即使按这4种发展方向升级优化了模型,也并没有解决“简单的数学模型与复杂的现实相脱节”这个根本的质疑。接下来本章后半部分的内容,就来探讨数学模型究竟在人文社科的研究中,扮演了怎样的角色。
二、关于数学在人文社科中的角色
0、数学模型的局限性
1894年,诺贝尔物理学奖得主、光速的测量者,阿尔伯特·迈克尔逊宣布:科学的大厦即将建成,人类将解开一切未解之谜。那时的科学家们坚信,自然界和人类社会的一切谜团,都能够用各种数学工具解开,包括微观的、原子化的个体行为是如何引发宏观的系统性行为的。
但是,随着研究的逐渐深入,科学家们发现,越来越多的现象,几乎不可能用一个简单的数学模型去描述。
比如:如何预测某地区一个月后的天气?如何预测股市的涨跌?
过去,科学家们认为,这些现象之所以难以预测,是因为影响变量太多,观测手段难以兼顾导致的。但随着研究的深入,科学家们逐渐发现,即便是非常简单的场景,复杂性和不可预测性也会产生。最典型的例子就是三体问题:三体问题不存在解析解。虽然我们可以用数值方法计算出任意时刻的数值解,但三体本质上是个混沌系统,任何一点轻微的扰动,都将令系统状态变得不可预测。
即便是存在解析解,能用简洁的初等函数表示,同时也不会导致模型不会过于复杂,也是一种奢望。例如, $\frac{sin(x)}{x}$ 的原函数、一元五次方程的求根公式,这些看似很简单的问题,其答案也已经是无法用初等函数表示得了的了。
这种复杂性,注定了对于现实中的很多问题,有解析解是一种偶然,有可用于数学建模的简洁解析解更是偶然中的偶然。在第3章中,一个由简单的“古诺模型”发展而来的模型,竟然频繁出现诸如
$ k<\frac{-13t^2+20t+5+\sqrt{(7t^2+4t+1)(31t^2-92t+73)}}{6(t+1)^2} $
类似的复杂内容,而这仅仅是添加了“权力”、“民智”这两个新概念、尚且没考虑本章第1节所提的那些拓展因素的结果。这毫无疑问也揭示了,数学模型在面对哲学社会科学问题时,很多时候是孤木难支的。
但这并不意味着人类面对未知就只能举手投降了。上世纪四五十年代,科学界曾经兴起了一场“控制论”运动,旨在研究微观的个体行为如何影响宏观的集体行为。经过数十年的发展,一场名为“复杂性科学”的思潮已经在整个科学界流行开来。这种专门研究“面对规律的不可预测性,人类应该采取何种应对手段”的思潮,深刻影响了自然科学和社会科学的研究范式。
1、应对方法一:放宽研究对象的尺度
尽管我们无法预测一个月后某个具体日期的天气,但我们至少可以根据气候特点判断当月的天气构成如何;尽管我们无法预测股市的波动,但我们可以从长远的视角研究资本主义的繁荣周期。这无疑向我们揭示了:只要适当放宽解释对象的尺度,那么尽管无法事无巨细地解释每一个细枝末节的现象,但简洁的模型已经足够揭示事物的规律。
在社会科学中,尺度的增大,意味着模型所需的解释变量的减少。一个个体在某一个时刻的具体行为受太多因素的影响,甚至很多时候可以说是随机的;但一个群体在一个时期内的行为策略已经很有章可循。如果要研究某一种经济现象对一个经济体内某些指标的影响,现代经济学已经有很成熟的理论模型。
但这里需要注意的是,尽管鼓励为了模型的简洁化而放宽尺度,但宏观的社会系统分析不能忽视其微观的社会成员行为基础,否则就会陷入卢卡斯批判(Lucas Critique)所言的情境:一切试图单纯靠历史数据来推演经济政策的影响都是天真的[9]。在吸取了“滞涨”的教训和卢卡斯批判的精神后,现代宏观经济学已经建立了多套以微观经济学为基础,分析宏观社会系统的理论体系。这也是未来整个社会科学界,想要实现理论的数理化、形式逻辑化,所要发展的方向。
2、应对方法二:放宽模型的精确度
前文举过三个例子,来表明现实中简洁的解析解是多么难得:三体问题、$\frac{sin(x)}{x}$的原函数、一元五次方程的求根公式
但科学家们并没有因此放弃。如果不追求完美的精度,这几个问题仍然有办法用简洁的模型来解决:三体问题可以把天体的坐标和速度展开为时间的级数形式的近似表达式;$\frac{sin(x)}{x}$也可以通过泰勒展开近似求解原函数;而一元五次方程,可以通过牛顿法等方式,在任意情况下都可以求得近似解。这意味着,如果不追求完全准确的精度,原本复杂甚至不可解的问题,也可以用相对简洁的模型来表示。
也正是因为同样的原理,尽管形如 $y=\vec{a}\cdot \vec{x}+b$的简单线性模型看似不符合实际,但在许多场合中其有效性已足以揭示某些规律。19世纪时,高斯就是使用最小二乘法拟合出的线性模型,计算出了一颗小行星的位置,并最终为观测所证实。
在方法层面,遇到过于复杂,难以求解出具体形式的概率密度函数,用特征函数来近似在大多数时候都是一种足以满足需要的方法。此外,遇到难以求解的偏微分方程,用变分法等方法求近似解,多数情况下也足够满足需求、指导实践。
在当今的社会科学中,面对复杂的人性和社会运行逻辑,牺牲模型的解释精度,换取一个清晰明了的揭示变量之间关系模型的做法已经并不罕见。越来越多的社会科学研究者已经不再单纯用 p 值或 R^2 值来评价模型的价值。
3、应对方法三:放宽模型的适用条件
尽管上一节论述了简单线性模型 $y=\vec{a}\cdot \vec{x}+b$ 的合理性,但这个模型毕竟建立在“变量之间的关系是线性的”这一假设之上,而这一严苛的适用条件在很多时候都会影响模型的有效性。
现实中,存在不少能在不严重牺牲模型的简洁性的基础上,放宽模型适用条件的方法。例如,在建模之前,对变量进行标准化和归一化,就可以消除量级和量纲的影响,放宽变量的正态性假设;而对模型进行一个简单的对数变换(即等式两边同时取对数)就可以令线性假设不那么严格。
正是在超越简单线性回归严苛条件的基础上,各种广义线性模型应运而生:
logistic回归超越了简单线性回归,将分析变量的范围拓展到了定类变量;
softmax回归又超越了logistic回归,具备了处理多分类问题的能力;
而在softmax回归的基础上,添加“隐藏层”这一要素,就形成了著名的深度学习神经网络。
是的,神经网络很复杂,复杂到它的可解释性都已经成了一团谜,但与混沌相比,它依然是简洁的。这种简洁伴随了适用条件的放宽,实现了模型的高度有效性。
4、应对方法四:重视经验资料
前面三种应对方案,都着眼于如何设计模型。但是,无论模型设计得多么精巧,它的有效性都是需要靠现实世界的数据来验证的。用贝叶斯学派的语言来描述就是:想要验证一个理论的有效性,那么无论这个理论模型设计得有多精妙,也只能提高理论成立的先验概率。而最终能检验理论的是后验概率,也就是经验资料的验证。
在自然科学中,面对复杂到无法靠建模来求解的问题,通常采取在实验室中做大量实验的方式来求解参数。拿隐形战斗机的设计来举例:战斗机的外形几乎不可能纯粹依靠流体力学模型来求解出最佳答案,必须通过大量的风洞实验来一步步试错,最终筛选出最合适的外形;而隐身涂料的布置方式,必须靠实验室中一次次雷达波的照射,才能试验出最佳的方案。在工程学领域,用类似大量实验的方式来求解参数、研究方案,是很常见的做法。
但是在社会科学中,作为基本研究对象的人,和自然科学中的微观粒子有着本质的不同:不同人的行为模式是有巨大的差异的,并且这种行为模式不可能像自然科学一样通过在实验室里反复实验探索出来。
由于研究对象的特殊性,社会科学常常面临着“科学性”不如自然科学的质疑。这对社会科学学者在定量方法的创新上提出了很高的要求,而社会科学在近百年的方法论创新上也取得了很多成果。例如,尽管无法在实验室里控制变量,精确揭示因果关系,但现今的社会科学方法论已经可以通过工具变量、双重差分、断点回归、合成控制等一系列手段进行因果推断,最大限度还原变量间的因果关系。诸如此类的经验资料解读方法上的创新,让社会科学研究者们,在无法像自然科学一样在实验室中做实验的情况下,依然最大程度上保证了学科的科学性。
而本专栏所讨论的权力、民智与自由的关系的问题,也可以在改进模型的基础上,通过对历史资料的科学分析,结合对现实因素的考察,得出一个相对科学的、能够最大限度保障公民自由的权力分配格局。这种基于逻辑推理和经验观察的分析路径,比“普世价值”之类的辩经式思维方式,要更科学,也更具有指导实践的价值。
参考
- ^Harsanyi John C, “Cardinal Welfare, Individualistic Ethics, and Interpersonal Comparisons of Utility”, Journal of Political Economics 63, 1955, p309-21.
- ^Harsanyi John C, “Nonlinear Social Welfare Functions”, Theory and Decision 6,1975 , p311-32
- ^Ng Yew-Kwang, “Bentham or Bergson? Finite Sensibility, Utility Functions and Social Welfare Functions”, Review of Economic Studies 42, 1975, p545-69.
- ^Ng Yew-Kwang, “Expected Subjective Utility: Is the Neumann-Morgenstern Utility the Same as the Neoclassical’s?”, Social Choice and Welfare1, 1984, p177-86.
- ^Luce R Duncan and Howard Raiffa, Games and Decisions, New York: Wiley, 1957.
- ^DeMeyer F and Charles Plott, “A Welfare Function Using Relative Intensity of Preference”, Quarterly Journal of Economics 85, 1971, p179-86.
- ^Kaneko Mamoru and Kenjiro Nakamura, “The Nash Social Welfare Function”, Econometrica 47, 1979, p423-35.
- ^详见Kahneman Daniel and Tversky Amos, “Prospect Theory: An Analysis of Decision under Risk”, Econometrica. 47 (2), 1979, p.263–91.
- ^这是因为,历史经济数据所对应的社会环境,和当今社会是不同的。这就导致从微观层面看,过去人们在当年的环境下所形成的行为模式未必能和今天的行为模式对应上,在此基础上试图从过去的宏观数据中汇总规律来预测当今的宏观数据毫无意义。详见Lucas Robert, “Econometric Policy Evaluation: A Critique” . In Brunner, K.; Meltzer, A. (eds.). The Phillips Curve and Labor Markets. Carnegie-Rochester Conference Series on Public Policy. Vol. 1. New York: American Elsevier, 1976, p19–46.