模型拓展

在上一章的结尾，我们已经通过数学的方式，证明了“只要博弈双方都是理性的，那么权力的存在必然会损害弱势方的自由”这个结论。但现实中，不但非理性的情况比比皆是，博弈双方理性程度存在明显差距的情况也不罕见。本章就来讨论，一旦引入非理性因素，对自由又会造成什么样的结果，是否存在帕累托改进的可能。

由于本章内容是上一章内容的延续拓展，因此本章章节标题序号衔接自上一章

三、考虑“民智”的情况

这里，我们假设弱势方B是非理性的（为了模型的简洁，这里不再假设A也是非理性的。事实上只要A的非理性程度远小于B，本章的数学结论依然成立，此处不再额外赘述），其对自己收益函数的观测存在误差，导致对 b 的观测有一定偏离。设偏离程度为 $b_{2}$ 。（同样为了模型的简洁，这里不再讨论对 a 偏离的情况。对 a 的偏离不影响本章的数学结论）

现在我们有三种施加权力前的收益函数了：

A的收益函数: $U_{A权力前}=(-a(x+y)+b)x$

B观测到的自己的收益函数: $U_{B观权力前}=(-a(x+y)+(b+b_{2}))y$

B实际的收益函数: $U_{B实权力前}=(-a(x+y)+b)y$

仿照第一节的步骤（注意，此时指导B行为的收益函数要以 $U_{B观权力前}$ 为准），可以算出A施加权力前，均衡解为：

$$ \begin{cases} x=\frac{b-b_{2}}{3a} \ y=\frac{b+2b_{2}}{3a} \end{cases} $$

上面的土黄色曲面为B观测到的自己的收益曲面，下面的蓝色曲面是B真正的收益曲面。红色的线为B的行动曲线

设 $t=\frac{b_{2}}{b}$ ，**代表行动者B的“愚蠢程度”**

1、t≤1的情况

可以看出，为了令x落在定义域之内，这里必须假设$ t\leq1$。若 t>1 ，意味着B已经蠢到了不需要A付出任何自由（即x到达定义域的边界：0），自己就会主动当韭菜贡献出大量自己的自由，此时A付出一丁点自由都是亏本。这种情况放到后面再讨论，这里先讨论 $t\leq1$的情况

带入计算可得：

$$ \begin{cases} U_{A权力前}=\frac{(b-b_{2})^{2}}{9a} \ U_{B观权力前}=\frac{(b+2b_{2})^{2}}{9a} \ U_{B实权力前}=\frac{(b-b_{2})(b+2b_{2})}{9a} \end{cases} $$

在现实中，弱势方对强势方的权力制衡，显然应与弱势方观测到的自己的收益期望相关，因此，A因权力制衡付出的成本应以$ U_{B观}$重新计算。解得

$$ E[U_{B观权力前}]-E[U_{B观权力后}]=\frac{(b+b_{2})^{2}}{12a}-\frac{(b+b_{2})p}{2}+ap^{2} $$

此时，施加权力后的收益函数变成了这三种：

$$ \begin{cases} U_{A权力后}=(-a(x+p)+b)x-k(\frac{(b+b_{2})^{2}}{12a}-\frac{(b+b_{2})p}{2}+ap^{2})\ U_{B观权力后}=(-a(x+p)+(b+b_{2}))p \ U_{B实权力后}=(-a(x+p)+b)p \end{cases} $$

仿照第二节的步骤，解得令权力施加者A的收益最大化的解为：

$$ \begin{cases} x=\frac{(3b-b_{2})k}{2a(4k-1)} \ p=\frac{k(b+b{2})-b}{a(4k-1)} \end{cases} $$

假设分母大于0，即 $k>\frac{1}{4}$ 。由于此处已规定$ t\leq1$ ，因此$ (3b-b_{2})k$必大于等于0，不必担心x因小于0而落入定义域之外。但对于p，需额外假设$ k\geq\frac{1}{1+t}$ ，以保证 $p\geq0$

（事实上，若$ k>\frac{1}{4}$的假设不满足，则帕累托改进是无解的，这个也很容易猜到：对权力的制衡越小，意味着强势方越能侵犯自由而不付出多大代价，小到一定程度就不可能令弱势方拥有多少自由；$t\leq1$ 时，若$k>\frac{1}{1+t}$的假设不满足，帕累托改进同样无解。这两部分详细的证明我会放在附录中，以备读者查验）。带入计算可得

$$ \begin{cases} U_{A权力后}=\frac{(7b^{2}-4bb_{2}+b_{2}^{2})k-(b+b_{2})^{2}k^{2}}{12a(4k-1)} \ U_{B观权力后}=\frac{(7b^{2}+10bb_{2}+3b_{2}^{2})k^{2}-(2b^{2}+9bb_{2}+3b_{2}^{2})k+2bb_{2}}{2a(4k-1)^{2}} \ U_{B实权力后}=\frac{(3b-b_{2})(bk+b_{2}k-b)k}{2a(4k-1)^{2}} \end{cases} $$

下面，重点来了：

和上一节一样，由于A需要保证施加权力的行为对自己造成了正向的收益，因此A必须令$ \Delta U_{A}>0$。此时的

$\Delta U_{A}=U_{A权力后}-U_{A权力前}=\frac{-b^{2}[3(t+1)^2k^{2}+(13t^2-20t-5)k-4(t-1)^2]}{36a(4k-1)}$

解得，若令$\Delta U_{A}>0$，则k需满足 $k<\frac{-13t^2+20t+5+\sqrt{(7t^2+4t+1)(31t^2-92t+73)}}{6(t+1)^2}$ ①

如果要实现帕累托改进，则需要B的实际收益 $\Delta U_{B实}>0$。此时的$\Delta U_{B实}=U_{B实权力后}-U_{B实权力前}=\frac{b^{2}[(55t^2-14t-5)k^2-(32t^2-25t+11)k+4t^2-2t-2]}{18a(4k-1)^2}$

解得，若令$\Delta U_{B实}>0$，则k需满足$k>\frac{32t^2-25t+11-3(3-t)(4t-1)}{2(55t^2-14t-5)}$ ②

（注：此处略有跳步，事实上k仍有其它解集，但其它解集均不能令$k>\frac{1}{4}$ 且$ k>\frac{1}{1+t}$成立，故此处省略其它解集，仅保留②式）

将①与②联立，求得当 t>0.57 时，①>②，k存在实数解。当 $t\leq0.57$ 时，由于B足够聪明，仅靠自己就可以赚得足够的实际收益，因而A施展权力的自私行为只会损害B的自由。但当 t>0.57 时，B的愚蠢已经不可忽视，A出于自利目的强迫B反而可能导致B的收益比自己行动时更高，实现了帕累托改进。

2、1<t≤3的情况

t>1 意味着权力前的均衡解 x<0 ，落在了定义域之外；t\leq3 意味着权力后的均衡解x仍落在定义域之内。此时权力前的最值解落在了定义域边缘，即x=0的位置。此时：

$$ \begin{cases} x=0 \ y=\frac{b+b_{2}}{2a} \end{cases} $$

代入计算可得

$$ \begin{cases} U_{A权力前}=0 \ U_{B观权力前}=\frac{(b+b_{2})^{2}}{4a} \ U_{B实权力前}=\frac{(b^2-b_{2}^2)}{4a} \end{cases} $$

权力后的三种收益函数较$ t\leq1$ 时不变。此时：

$$ \Delta U_{A}=U_{A权力后}-U_{A权力前}=\frac{-b^{2}k[(t+1)^2k-(t^2-4t+7)]}{36a(4k-1)} $$

令$\Delta U_{A}>0$，解得 $k<\frac{t^2-4t+7}{(1+t)^2}$ ①

$$ \Delta U_{B实}=U_{B实权力后}-U_{B实权力前}=\frac{b^{2}[(14t^2+4t-10)k^2-(8t^2-2t-2)k+t^2-1]}{4a(4k-1)^2} $$

解得，若令$\Delta U_{B实}>0$，则k需满足$k>\frac{8t^2-2t-2+3(3-t)\sqrt{2t^2-1}}{2(14t^2+4t-10)}$ ②

联立①和②，解得，当 t<2.51 时，①>②，k存在实数解

综上，当 $t\geq2.51$ 时，由于B过于愚蠢，收益太低，必须有极高的权力制衡系数k来增加B的收益，才可以令B权力之后的自由大过权力之前，但这势必将损害A的自由，导致A拒绝施展权力。但当 t<2.51 时，B已经不那么愚蠢，B在权力之下弥补因自己的愚蠢造成的损失同时也会令A享受权力带来的额外收益，实现了帕累托改进。

但到此为止还没完，由于需要令p落入定义域内，因此前文规定了$k>\frac{1}{1+t}$③

联立①和③，解得，当 t<2 时，①>③，k存在实数解

（$ k\leq\frac{1}{1+t}$的情况对本章结论无重要影响，我将放到附录再讨论）

3、t＞3的情况

t>3 意味着权力之后的x仍然落在定义域之外，此时A最好的策略就是令x=0，和权力前一模一样。这就是说B已经愚蠢到不需要A动用任何权力，就能令A不劳而获，且这种不劳而获就是最优的状态。这种情况显然不属于帕累托改进，因而无需过多讨论

4、结论

结合1、2、3节的结论，可以得出：当B的“愚蠢程度”t满足 0.57<t<2 时，存在权力制衡系数k，使得A出于自利目的施展权力的行为同时也能令B获益，从而实现帕累托改进

这条结论，可以为部分现实中的政治现象提供合法性支持

例如，施加权力制止极端环保主义或恐怖主义的宣传流入民间，封禁他们的宣传路径，乃至在民众面前编造一些他们实际并未干过的恶行，是否正义？

这种行为明面上看侵犯了民众的知情权，但若民众缺乏足够的判断力，受到了蛊惑后认可了这些宣传，他们反而会做一些最终看来会侵犯自己自由的行为。因而，动用权力来“侵犯”民众知情的自由，反而可能会更多地保护他们的自由

四、考虑“民智的进步”的情况

如果本专栏仅仅到第三节为止，那么这个理论很有可能被专制主义利用，为专制的合法性作辩护：你看，既然民智未开的时候，对他们施加权力也能对他们有好处，那这种时候当然保持我的威权体制就好了。

可现实真是如此吗？别忘了，在持续多回合的博弈后，民智是会在不断学习、总结经验中进步的，即B的“愚蠢程度”t会随着时间的推移变得越来越小。这种情况下，权力制衡系数k应当如何变化才更合理？

在这里，我们采取一种罗尔斯主义的分析导向：以最大化弱势方B的利益为目标，分析k应如何变化

首先从B较为“愚蠢”的时间点开始分析，即t较大时。

1、1<t<2时

根据上一节，此时 U_{B实权力后}（后文简写为U_{B}）=\frac{(3b-b_{2})(bk+b_{2}k-b)k}{2a(4k-1)^{2}}

分别对k和t求偏导，可得

$$ \begin{cases} \frac{\partial U_{B}}{\partial t}=\frac{-b^2k[2k(t-1)-1]}{2a(4k-1)^2} \ \frac{\partial U_{B}}{\partial k}=\frac{b^2(t-3)[2k(t-1)-1]}{2a(4k-1)^3} \end{cases} $$

令二者等于0，可求得 k^*=\frac{1}{2(t-1)} 。带入可求得此时 U_{B^*}=\frac{b^2}{8a}

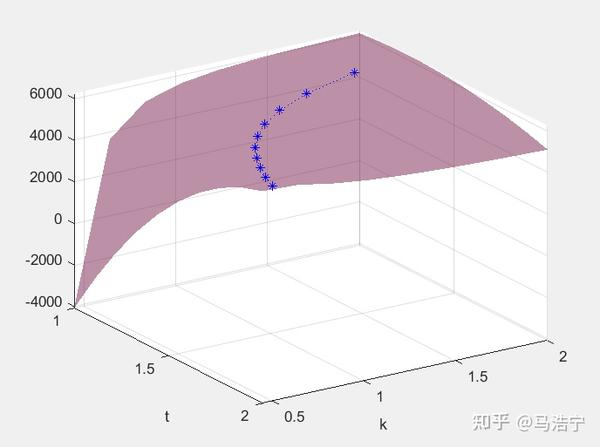
UB、t、k关系图。蓝色曲线即为$k*=1/[2(t-1)]$

显然，k与t成反比。若维持 $k^=\frac{1}{2(t-1)}$ 的关系，需要在t减少时，k*增加。

因此，只需要证明 $U_{B^*}$是极大值，就能得出结论：随着t的减少，维持B的最大利益的k*值越大

通过求二阶偏导，可得海森矩阵：

$$ H=\begin{pmatrix} \frac{b(3-t)[8k(t-1)+t-7]}{a(4k-1)^4}&\frac{b^2[4k(t-2)-1]}{2a(4k-1)^3}\ \frac{b^2[4k(t-2)-1]}{2a(4k-1)^3}&\frac{-b^2k^2}{a(4k-1)^2}\ \end{pmatrix} $$

其行列式

$$ \left| H \right|=\frac{b^4[2k(t-1)-1][16k^2(t-3)-2k(3t-7)+1]}{4a^2(4k-1)^6} $$

不幸的是，将$k^*=\frac{1}{2(t-1)}$ 带入$ \left| H \right|$ ，得出$ \left| H \right|=0$ 。也就是说，我们无法通过传统的通过海森矩阵行列式判定$ U_{B^*}$ 是否是极大值

但此时仍然有简便方法：只需证明“$ k^*=\frac{1}{2(t-1)}$上的点，若向不同方向变化，则无论什么方向， $U_{B}$均会降低”即可

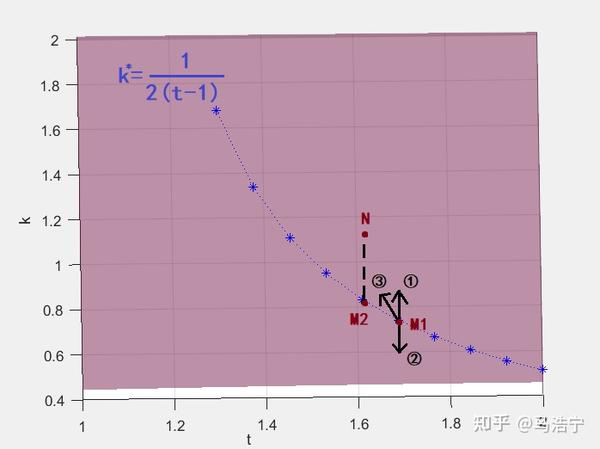
若曲线$k^*=\frac{1}{2(t-1)}$上的点M1欲向①方向移动（即t不变，k上升）。此时 $k>\frac{1}{2(t-1)}$ ，解得$ \frac{\partial U_{B}}{\partial k}<0$，即随着k的增加， $U_{B}$将降低。故①方向上$U_{B}$将减少

若曲线$ k^*=\frac{1}{2(t-1)} $上的点M1欲向②方向移动（即t不变，k下降）。此时 $k<\frac{1}{2(t-1)}$，解得$ \frac{\partial U_{B}}{\partial k}>0 $ ，即随着k的降低， $U_{B}$ 将降低。故②方向上$U_{B}$将减少

若曲线$k^*=\frac{1}{2(t-1)}$上的点M1欲向N点所在的③方向移动（即t、k均移动）。此时可过N点做一条铅垂线，与曲线交于M2点。通过重复以上步骤，可知N点的U_{B}必小于M2点。由于曲线上的$U_{B}\equiv\frac{b^2}{8a}$，M2点与M1点U_{B}值相同，故③方向上的$U_{B}$仍将减少

综上，曲线$k^*=\frac{1}{2(t-1)}$是$U_{B}$的极大值线

现在，我们可以得出结论：当 1<t<2 时随着t的减少，维持B的最大利益的k值越大。并且由于$ t\rightarrow1$ 时，$k^=\frac{1}{2(t-1)}\rightarrow+\infty $，因此对于任意$ k_{0}$ ，必存在 k'>k_{0} ，使得随着t的持续降低， $ U_{B}(k=k')>U_{B}(k=k_{0}) $

综上所述，当B的“愚蠢程度”t在 (1,2) 时，随着民智的开化，对强势者A的权力制衡越强，越能保护弱势者B的利益

2、0.57<t≤1时

由于$ t\leq1$ ，此时可轻易算出：

$$ \begin{cases} \frac{\partial U_{B}}{\partial t}>0 \ \frac{\partial U_{B}}{\partial k}>0 \end{cases} $$

故随着民智的开化（t越来越低），$U_{B}$将越来越低。此时唯有提高对A的权力制衡（即提高k），才能维持B的利益

3、结论

由于t在 $(0.57,1]\cup(1,2)$上的结论相同，且$U_{B}$在该区间内连续。故可以得出以下结论：

尽管民智未开时，适度的权威有助于保障民众的自由。但随着民智的逐渐开化，应逐渐降低权威，才能最大限度保障人民的自由

这个模型的数学部分到此基本结束。显然，它还有很多不完美的地方：比如它和古诺模型中的“企业”概念一样，将“强势方”、“弱势方”视作了有统一集体行动的主体；比如它只分析了两方博弈的场景；比如它简单地假设民智是线性成长的，等等。它有创新的地方、也有明显的局限性，因而必须谨慎地看待它的价值。关于这个模型的价值、不完善的方面以及未来可能的发展方向，我将放在第4章进行统一讨论。